题目内容
 如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是
如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是26
26
.分析:由题意可知:阴影部分的面积=S△FNB-S△CFM-S△PBE,求S△FED的面积需要知道BF的长度,求S△CFM和S△PBE需要求出FC和BE的长度,由“BC=10,EF=8,CE=FC+BE”可知:2FC+BE=8①,2BE+FC=10②,由①和②即可求出FC和BE的值,从而问题逐步得解.
解答:解:由题意可知:2FC+BE=8①,
2BE+FC=10②,
由①得:BE=8-2FC③,
将③代入②得:
2×(8-2FC)+FC=10,
16-4FC+FC=10,
3FC=6,
FC=2;
BE=8-2×2=4;
所以BF=2×(2+4),
=2×6,
=12;
阴影部分的面积=
×12×(
×12)-
×2×2-
×4×4,
=6×6-2-8,
=36-10,
=26;
故答案:26.
2BE+FC=10②,
由①得:BE=8-2FC③,
将③代入②得:
2×(8-2FC)+FC=10,
16-4FC+FC=10,
3FC=6,
FC=2;
BE=8-2×2=4;
所以BF=2×(2+4),
=2×6,
=12;
阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=6×6-2-8,
=36-10,
=26;
故答案:26.
点评:解答此题关键是先求出FC和BE的长度,进而利用阴影部分的面积=S△FNB-S△CFM-S△PBE,即可求解.

练习册系列答案
相关题目
 (2012?宜丰县模拟)如图所示,两个相同的直角三角形部分叠在一起.求阴影部分的面积.(单位:厘米)
(2012?宜丰县模拟)如图所示,两个相同的直角三角形部分叠在一起.求阴影部分的面积.(单位:厘米) 用四个大小相等的等腰直角三角形边与边相拼接,可以拼出多少个不同的图形?(一个图形经过平移、旋转、翻折后不作为另一个图形,如图所示的两个图形看作是相同的图形.)
用四个大小相等的等腰直角三角形边与边相拼接,可以拼出多少个不同的图形?(一个图形经过平移、旋转、翻折后不作为另一个图形,如图所示的两个图形看作是相同的图形.) 如图 所示的两个同心圆的半径分别为R 和r,R 和r 都是自然数,若圆环(阴影部分)的面积是493π,则R-r=
如图 所示的两个同心圆的半径分别为R 和r,R 和r 都是自然数,若圆环(阴影部分)的面积是493π,则R-r=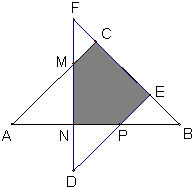 如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是________.
如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是________.