题目内容
如图，∠D=2∠B，∠C=2∠A，∠A=60°，求∠B，∠C，∠D．分析：先根据∠C=2∠A，∠A=60°，可求∠C的度数；可设∠B=x，则由已知条件可得∠D=2x，根据四边形的内角和等于360°即可列出方程求解即可．
解答：解：∠C=2∠A=120°．
设∠B=x，则∠D=2x，依题意有：
x+2x=360°-（60°+120°），
3x=360°-180°，
3x=180°，
x=60°；
2x=2×60°=120°．
答：∠B为60°，∠C为120°，∠D为120°．
设∠B=x，则∠D=2x，依题意有：
x+2x=360°-（60°+120°），
3x=360°-180°，
3x=180°，
x=60°；
2x=2×60°=120°．
答：∠B为60°，∠C为120°，∠D为120°．
点评：考查了多边形的内角和，解题的关键是根据四边形的内角和等于360°得到方程x+2x=360°-（60°+120°）．
练习册系列答案
相关题目
如图，四边形ABCD，∠A+∠C=210°，∠D=2∠B，求∠B．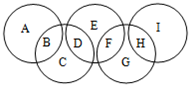
如图，A，B，C，D，E，F，G，H，I代表九个各不相同的正整数，A，B，C，D，E，F，G，H，I的总和为2008，并且每个圆中所填数的和都等于M．
如图，A至B是下坡，B至C是平路，C至D是上坡．小张和小王在上坡时步行速度是每小时4千米，平路时步行速度是每小时5千米，下坡时步行速度是每小时6千米．小张和小王分别从A和D同时出发，2小时后两人在E点相遇．已知E在BC上，并且E至C的距离是B至C距离的
如图中，A→B→C→D→E→A是小凤的行走路线图．在括号里填上表示B、C、D、E位置的数字．