题目内容
3-5+7-9+11-13…+1995-1997+1999=
181×
11=
1001
1001
．
| ||
| 963个0 |
| ||
| 1028个0 |
0.00…01991（小数部分共有1990个0）．
0.00…01991（小数部分共有1990个0）．
．分析：（1）式子里都是2000内的奇数，2000以内共1000个奇数，少个1就总共999个数字，除去第1个数字，每相邻两个数字的差是2，共（999-1）÷2=499对数字，和是499×2=998，998+3=1001；
（2）先把小数非0的数相乘，得到结果和小数的位数，然后再把两个小数中0的个数相加，减去整数部分的两个0，得到小数部分0的个数．
（2）先把小数非0的数相乘，得到结果和小数的位数，然后再把两个小数中0的个数相加，减去整数部分的两个0，得到小数部分0的个数．
解答：解：（1）3-5+7-9+11-13…+1995-1997+1999，
=3+（7-5）+（11-9）+…+（1999-1997），
=3+2×499，
=3+998，
=1001；
（2）181是三位，11是两位，相乘后181×11=1991是四位，三位加两位是五位小数，因此1991前面还要添一个0，
又963+1028=1991，1991-2（整数部分的0）+1=1990，
所以0.00…0181（963个0）×0.00…011（1028个0）=0.00…01991（小数部分共有1990个0）．
故答案为：1001，0.00…01991（小数部分共有1990个0）．
=3+（7-5）+（11-9）+…+（1999-1997），
=3+2×499，
=3+998，
=1001；
（2）181是三位，11是两位，相乘后181×11=1991是四位，三位加两位是五位小数，因此1991前面还要添一个0，
又963+1028=1991，1991-2（整数部分的0）+1=1990，
所以0.00…0181（963个0）×0.00…011（1028个0）=0.00…01991（小数部分共有1990个0）．
故答案为：1001，0.00…01991（小数部分共有1990个0）．
点评：第（1）题，关键是观察出：除去第1个数字，每相邻两个数字的差是2；
第（2）题，此题关键是弄清小数中“0”的个数．
第（2）题，此题关键是弄清小数中“0”的个数．
练习册系列答案
相关题目
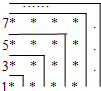（2011?白山模拟）先观察再填充．
数形结合是一种重要的数学思想，认真观察右上图形，然后完成下列问题：