题目内容
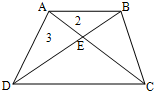 如图,梯形ABCD中,△ABE和△ADE的面积分别是2cm2,3cm2.△CDE的面积是
如图,梯形ABCD中,△ABE和△ADE的面积分别是2cm2,3cm2.△CDE的面积是4.5
4.5
cm2.分析:观察图形可知,△ABE和△ADE的面积分别是2cm2,3cm2,因为平行线间的距离处处相等,所以根据高一定时,三角形的面积与底成正比例的性质可得△BEC和△ADE的面积相等,也是3cm2,则△ABE和△BEC的面积比是2:3,所以可得AE:EC=2:3,所以可得△ADE和△CDE的面积比是2:3,据此即可求出△CDE
解答:解:,△ABE和△ADE的面积分别是2cm2,3cm2,
因为平行线间的距离处处相等,所以可得△BEC和△ADE的面积相等,也是3cm2,
则△ABE和△BEC的面积比是2:3,
所以可得AE:EC=2:3,
所以△ADE和△CDE的面积比是2:3,
则△CDE的面积是:
×3=4.5(cm2),
答:△CDE的面积是4.5cm2.
故答案为:4.5.
因为平行线间的距离处处相等,所以可得△BEC和△ADE的面积相等,也是3cm2,
则△ABE和△BEC的面积比是2:3,
所以可得AE:EC=2:3,
所以△ADE和△CDE的面积比是2:3,
则△CDE的面积是:
| 3 |
| 2 |
答:△CDE的面积是4.5cm2.
故答案为:4.5.
点评:此题主要考查高一定时,三角形的面积与底成正比例的性质的灵活应用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 (2012?北京)如图:梯形ABCD中,AD∥BC,AC、BD交于M,
(2012?北京)如图:梯形ABCD中,AD∥BC,AC、BD交于M,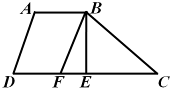 如图,梯形ABCD中,上底AB的长度是10厘米,梯形的高BE的长度是12厘米,且E是CD中点,BF将梯形ABCD分成面积相等的两部分.那么,EF的长度是
如图,梯形ABCD中,上底AB的长度是10厘米,梯形的高BE的长度是12厘米,且E是CD中点,BF将梯形ABCD分成面积相等的两部分.那么,EF的长度是 如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?
如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?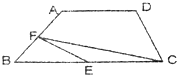 如图,梯形ABCD中,BC=2AD,E、F分别为BC、AB的中点.连接EF、FC.
如图,梯形ABCD中,BC=2AD,E、F分别为BC、AB的中点.连接EF、FC.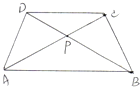 如图在梯形ABCD 中,AB平行于CD,AC与BD 相交于点P,则图中面积相等的三角形共有
如图在梯形ABCD 中,AB平行于CD,AC与BD 相交于点P,则图中面积相等的三角形共有