题目内容
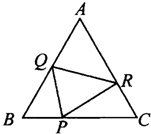 如图,等边三角形ABC 的面积为1,且BP=
如图,等边三角形ABC 的面积为1,且BP=| 1 |
| 2 |
| 5 |
| 18 |
| 5 |
| 18 |
分析:(1)连接CQ,因为三角形ABC是等边三角形,且AQ=BQ,可得三角形BQC和三角形AQC的面积相等都等于
,根据高一定时,三角形的面积与底成正比的关系可得:三角形QCR和三角形BQP的面积相等,由此可得:四边形PCRQ的面积=三角形BPQ的面积+三角形QCP的面积=
,只要再求出三角形PCR的面积即可解决问题;
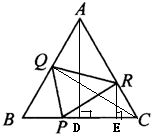
(2)分别过点R、A画出BC边上的高线RE、AD,则RE∥AD,所以可得:RE:AD=CR:AC=1:3,又因为PC:BC=2:3,所以三角形PCR与三角形ABC的面积的比是
×
=
,所以三角形PCR的面积是
;
由上述分析即可得出三角形PRQ的面积为:
-
=
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)分别过点R、A画出BC边上的高线RE、AD,则RE∥AD,所以可得:RE:AD=CR:AC=1:3,又因为PC:BC=2:3,所以三角形PCR与三角形ABC的面积的比是
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 9 |
由上述分析即可得出三角形PRQ的面积为:
| 1 |
| 2 |
| 2 |
| 9 |
| 5 |
| 18 |

解答:解:连接CQ,根据题干分析可得:
四边形PCRQ的面积=
,
分别过点R、A画出BC边上的高线RE、AD,则RE∥AD,
所以可得:RE:AD=CR:AC=1:3,
又因为PC:BC=2:3,
所以三角形PCR与三角形ABC的面积的比是
×
=
,
所以三角形PCR的面积是:1×
=
;
三角形PRQ的面积为:
-
=
.
故答案为:
.
四边形PCRQ的面积=
| 1 |
| 2 |
分别过点R、A画出BC边上的高线RE、AD,则RE∥AD,
所以可得:RE:AD=CR:AC=1:3,
又因为PC:BC=2:3,
所以三角形PCR与三角形ABC的面积的比是
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
所以三角形PCR的面积是:1×
| 2 |
| 9 |
| 2 |
| 9 |
三角形PRQ的面积为:
| 1 |
| 2 |
| 2 |
| 9 |
| 5 |
| 18 |
故答案为:
| 5 |
| 18 |
点评:此题反复考查了高一定时,三角形的面积与底成正比的关系,得出四边形PCRQ的面积是这个三角形面积的一半,从而把求三角形PRQ的面积转变成求三角形PCR的面积,这是解决本题的关键.

练习册系列答案
相关题目
 如图中由等边三角形ABO,AOD,DOC围成的等腰梯形,它的面积是1,又知M是AB的中点,那么△COM面积等于多少?
如图中由等边三角形ABO,AOD,DOC围成的等腰梯形,它的面积是1,又知M是AB的中点,那么△COM面积等于多少?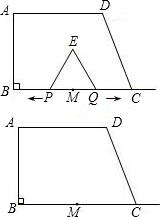
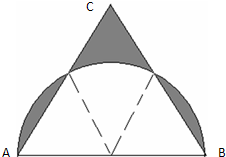 已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14)
已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14) 如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.
如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.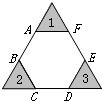 如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为
如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为