题目内容
 如图,△ABC中,OC=OF,S△AFO=4,S△OCE=1,求三角形ABC的面积.
如图,△ABC中,OC=OF,S△AFO=4,S△OCE=1,求三角形ABC的面积.分析:(1)OF=OC,则三角形AOF和三角形AOC的面积相等,由此可得:三角形AOC的面积是4,三角形AOE的面积是4-1=3;且三角形BOF的面积=三角形BOC的面积=
三角形BFC的面积;
(2)根据高一定时,三角形的面积与底成正比的性质,可得:三角形AOB的面积:三角形AOE的面积=三角形BOC的面积:三角形COE的面积=BO:EO;由此设三角形BFO和三角形BOC的面积就是x,由此即可列出比例式解答即可.

| 1 |
| 2 |
(2)根据高一定时,三角形的面积与底成正比的性质,可得:三角形AOB的面积:三角形AOE的面积=三角形BOC的面积:三角形COE的面积=BO:EO;由此设三角形BFO和三角形BOC的面积就是x,由此即可列出比例式解答即可.

解答:解:OF=OC,则三角形AOC面积=三角形AOF的面积=4;
则三角形AOE的面积=4-1=3;
设三角形BFO和三角形BOC的面积为x,
则
=
;
3x=4+x,
2x=4,
x=2,
则三角形BCF的面积为2+2=4,
所以三角形ABC的面积为:4+4+4=12.
答:三角形ABC的面积是12.
则三角形AOE的面积=4-1=3;
设三角形BFO和三角形BOC的面积为x,
则
| 4+x |
| 3 |
| x |
| 1 |
3x=4+x,
2x=4,
x=2,
则三角形BCF的面积为2+2=4,
所以三角形ABC的面积为:4+4+4=12.
答:三角形ABC的面积是12.
点评:此题是利用代数思想解答几何图形的面积问题,这里反复考查了高一定时,三角形与底成正比的性质的灵活应用.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图,O为△ABC的边AB上的一点,分别连接OD,OE,…,OQ,则图中共有
如图,O为△ABC的边AB上的一点,分别连接OD,OE,…,OQ,则图中共有
 如图,在△ABC中,已知M、N分别在AC、BC上,BM与AN相交与O.若△AOM,△ABO和△OBN的面积分别是3、2、1.求△MNC的面积.
如图,在△ABC中,已知M、N分别在AC、BC上,BM与AN相交与O.若△AOM,△ABO和△OBN的面积分别是3、2、1.求△MNC的面积.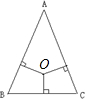 如图,三角形ABC中有一点O,O点到三条边的垂线段长都是3厘米.又知道三角形的周长是30厘米,那么三角形ABC的面积是
如图,三角形ABC中有一点O,O点到三条边的垂线段长都是3厘米.又知道三角形的周长是30厘米,那么三角形ABC的面积是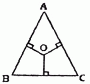 如图,在三角形ABC中有一点O,O点到三条边的垂线长都是2厘米,又知道三角形的周长是20厘米,那么三角形ABC的面积是
如图,在三角形ABC中有一点O,O点到三条边的垂线长都是2厘米,又知道三角形的周长是20厘米,那么三角形ABC的面积是