题目内容
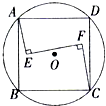 如图,圆O内有一个正方形ABCD.正方形内有一折线段.其中AE⊥EF,EF⊥FC.并且AE=4.EF=9,FC=8,则圆的面积为
如图,圆O内有一个正方形ABCD.正方形内有一折线段.其中AE⊥EF,EF⊥FC.并且AE=4.EF=9,FC=8,则圆的面积为分析:首先连接AC,则可证得△AEM∽△CFM,根据相似三角形的对应边成比例,即可求得EM与FM的长,然后由勾股定理求得AM与CM的长,AC的长即为圆的直径,然后再根据圆的面积公式进行计算即可得解.
解答:解:
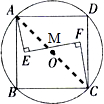
连接AC,
∵AE丄EF,EF丄FC,
∴∠E=∠F=90°,
∵∠AME=∠CMF,
∴△AEM∽△CFM,
=
=
,
AE=4.EF=9,FC=8,
=
=
,
EM=3,FM=6,
在Rt△AEM中,AM2=AE2+EM2,AM=
=5,
在Rt△FCM中,CM2=CF2+FM2,CM=
=10,
所以AC=5+10=15,
圆的面积为:π(
)2=56.25π,
答:图中圆的面积为56.25π.
故答案为:56.25π.

连接AC,
∵AE丄EF,EF丄FC,
∴∠E=∠F=90°,
∵∠AME=∠CMF,
∴△AEM∽△CFM,
| AE |
| FC |
| EM |
| FM |
| AM |
| CM |
AE=4.EF=9,FC=8,
| EM |
| FM |
| 4 |
| 8 |
| 1 |
| 2 |
EM=3,FM=6,
在Rt△AEM中,AM2=AE2+EM2,AM=
| 16+9 |
在Rt△FCM中,CM2=CF2+FM2,CM=
| 64+36 |
所以AC=5+10=15,
圆的面积为:π(
| 15 |
| 2 |
答:图中圆的面积为56.25π.
故答案为:56.25π.
点评:此题考查了相似三角形的判定与性质,圆的面积的求解方法,以及勾股定理的应用.此题综合性较强,解题时要注意数形结合思想的应用.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 如图,在长方形内有一个最大的三角形.请你首先在图中量出所需数据标在图上,然后求出三角形的面积.(可在图中添上你需要的线)
如图,在长方形内有一个最大的三角形.请你首先在图中量出所需数据标在图上,然后求出三角形的面积.(可在图中添上你需要的线)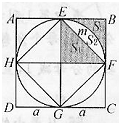 如图,边长为2a的正方形ABCD内有一个最大的圆圆O,圆O内有一个最大的正方形EFGH.用S1,S2,S3依次表示△EOF的面积,弓形EmF的面积,带弧边EmF的△EBF的面积,则S1*S2*S3=
如图,边长为2a的正方形ABCD内有一个最大的圆圆O,圆O内有一个最大的正方形EFGH.用S1,S2,S3依次表示△EOF的面积,弓形EmF的面积,带弧边EmF的△EBF的面积,则S1*S2*S3= 如图,圆O内有一个正方形ABCD.正方形内有一折线段.其中AE⊥EF,EF⊥FC.并且AE=4.EF=9,FC=8,则圆的面积为________(结果保留π).
如图,圆O内有一个正方形ABCD.正方形内有一折线段.其中AE⊥EF,EF⊥FC.并且AE=4.EF=9,FC=8,则圆的面积为________(结果保留π). 如图,边长为2a的正方形ABCD内有一个最大的圆圆O,圆O内有一个最大的正方形EFGH.用S1,S2,S3依次表示△EOF的面积,弓形EmF的面积,带弧边EmF的△EBF的面积,则S1*S2*S3=________.(圆周率π取3)
如图,边长为2a的正方形ABCD内有一个最大的圆圆O,圆O内有一个最大的正方形EFGH.用S1,S2,S3依次表示△EOF的面积,弓形EmF的面积,带弧边EmF的△EBF的面积,则S1*S2*S3=________.(圆周率π取3)