题目内容
 如图,在△ABC中,DC=3BD,DE=EA,若△ABC面积是2,则阴影部分的面积是
如图,在△ABC中,DC=3BD,DE=EA,若△ABC面积是2,则阴影部分的面积是| 6 |
| 7 |
| 6 |
| 7 |
分析:连接辅助线DF
 S四边形AFCD=S阴影×2,(AE=DE 三角形等底等高) ①因为S△AEF=S△DEF,所以 S阴影=S△DFC 又S△BDF=
S四边形AFCD=S阴影×2,(AE=DE 三角形等底等高) ①因为S△AEF=S△DEF,所以 S阴影=S△DFC 又S△BDF=
S△DFC=
S阴影,(DC=3BD,三角形等高底为3倍)②①+②AFCD面积+三角形BDF面积=2×S阴影+
S阴影=2所以S阴影=
.
 S四边形AFCD=S阴影×2,(AE=DE 三角形等底等高) ①因为S△AEF=S△DEF,所以 S阴影=S△DFC 又S△BDF=
S四边形AFCD=S阴影×2,(AE=DE 三角形等底等高) ①因为S△AEF=S△DEF,所以 S阴影=S△DFC 又S△BDF=| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 6 |
| 7 |
解答:解:连接DF,则S四边形AFCD=2×S阴影,
又DC=3BD,所以S△BDF=
S△DFC=
S阴影,
因此S四边形AFCD+S△BDF=2×S阴影+
S阴影,
即:S△ABC=
S阴影.
所以S阴影=2÷
=
.
故答案为:
.
又DC=3BD,所以S△BDF=
| 1 |
| 3 |
| 1 |
| 3 |
因此S四边形AFCD+S△BDF=2×S阴影+
| 1 |
| 3 |
即:S△ABC=
| 7 |
| 3 |
所以S阴影=2÷
| 7 |
| 3 |
| 6 |
| 7 |
故答案为:
| 6 |
| 7 |
点评:此题考查了三角形的面积与底的正比关系,在做题时应理清关系.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 如图,在△ABC中,D为BC边上任一点,AE=
如图,在△ABC中,D为BC边上任一点,AE= 如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE=
如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE= (2013?北京模拟)如图,在△ABC中,AD=
(2013?北京模拟)如图,在△ABC中,AD= 如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?
如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?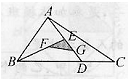 如图,在△ABC中,
如图,在△ABC中,