题目内容
圆周上均匀地放置了100枚棋子,其中黑棋子48枚,白棋子52枚.若将圆周上任意两枚棋子变换位置称为一次对换,那么最少要经过
24
24
次对换可使黑棋子在圆周上互不相邻(两枚黑棋子之间至少有一枚白棋子).分析:因为是要求“最少”,因此可考虑极端情况,如果开始的时候是黑棋子的旁边都是黑棋子,白棋子的旁边都是白棋子(除了交界外的4个棋子),需要移开24枚黑色棋子,因为同色棋子对换与没有对换一样,所以即至少经过24次对换.
解答:解:最极端的情况是48枚黑棋子全部相邻,此时,需要移开24枚黑色棋子,因为同色棋子对换与没有对换一样,所以即至少经过24次对换,才可使黑棋子在圆周上互不相邻.
点评:可以这样理解:黑棋最后的排列是48枚相连,开始时至少有一个48连中存在24个黑棋,需要改变另外的24个,所以需要24次.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
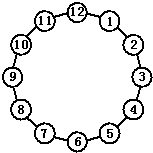 如图,一个圆盘上均匀地依次表示第1、2、3、…、12个洞.有一只小虫从1号洞按顺时针方向起跳,规定它跳的步数是它起跳洞的数码.例如,第1次从第1洞跳到第1洞,第2次从第2洞跳2步到第4洞,第3次从第4洞起跳,跳4步到第8洞,….第m次从第x洞起跳,跳x步,如果小虫按照这个规则从第1洞起跳,跳了100次到第N(N=1、2、3、…12)洞,则它共跳了多少步?N是几?
如图,一个圆盘上均匀地依次表示第1、2、3、…、12个洞.有一只小虫从1号洞按顺时针方向起跳,规定它跳的步数是它起跳洞的数码.例如,第1次从第1洞跳到第1洞,第2次从第2洞跳2步到第4洞,第3次从第4洞起跳,跳4步到第8洞,….第m次从第x洞起跳,跳x步,如果小虫按照这个规则从第1洞起跳,跳了100次到第N(N=1、2、3、…12)洞,则它共跳了多少步?N是几?