题目内容
如图，已知AB=16cm，图中的曲线是由半径不同的三种半圆弧平滑连接而成，那么阴影部分的面积是________cm2．（π取3.14）
100.48
分析：如图所示，将空白部分②旋转平移到阴影部分①的位置，则会得到一个直径为
AB的半圆，同样的方法，对其他相同的空白图形进行旋转平移，这样共得到两个直径为AB的圆，于是可以看出阴影部分的面积=以AB为直径的圆的面积-2个以AB为直径的圆的面积，AB的值已知，于是问题得解．
解答：阴影部分的面积：
3.14×（16÷2）2-2×3.14×（×16÷2）2，
=3.14×64-6.28×16，
=200.96-100.48，
=100.48（平方厘米）；
答：阴影部分的面积是100.48平方厘米．
故答案为：100.48．
点评：解答此题的关键是：利用旋转平移的方法，得到小圆的直径与大圆的直径的关系，进而得出：阴影部分的面积=以AB为直径的圆的面积-2个以AB为直径的圆的面积．
分析：如图所示，将空白部分②旋转平移到阴影部分①的位置，则会得到一个直径为
AB的半圆，同样的方法，对其他相同的空白图形进行旋转平移，这样共得到两个直径为AB的圆，于是可以看出阴影部分的面积=以AB为直径的圆的面积-2个以AB为直径的圆的面积，AB的值已知，于是问题得解．解答：阴影部分的面积：
3.14×（16÷2）2-2×3.14×（
×16÷2）2，=3.14×64-6.28×16，
=200.96-100.48，
=100.48（平方厘米）；
答：阴影部分的面积是100.48平方厘米．
故答案为：100.48．
点评：解答此题的关键是：利用旋转平移的方法，得到小圆的直径与大圆的直径的关系，进而得出：阴影部分的面积=以AB为直径的圆的面积-2个以
AB为直径的圆的面积． 
练习册系列答案
ABC考王全优卷系列答案
相关题目
每天，小明上学都要经过一段平路AB、一段上坡路BC和一段下坡路CD（如图），已知AB：BC：CD=1：2：1，并且小明在平路、上坡路、下坡路上的速度比为3：2：4，那么小明上学与放学回家所用的时间比是
如图，以BC为直径画半圆，A是圆弧上一点，分别以AB，AC为直径画半圆，围成月牙形1和月牙形2．已知：BC=20厘米，AB=12厘米，AC=16厘米．（注：此时∠BAC是直角）
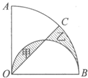
如图，以BC为直径画半圆，A是圆弧上一点，分别以AB，AC为直径画半圆，围成月牙形1和月牙形2．已知：BC=20厘米，AB=12厘米，AC=16厘米．（注：此时∠BAC是直角）