Question

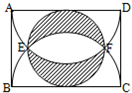如图中，AB=3，阴影部分的面积是

4.5

．

Answer 1

分析：如下图，找出中间的圆与矩形相切的交点G、H，连接E、F，连接G、H，连接E、G，连接G、F，EF和GH的交点为O，显然O是中间的圆的圆心，GH和EF是中间圆的直径，长度为AB的长，H是上个大半圆的圆心，G是下个大半圆的圆心，在△EGF中EO=FO=GO=

3

2

，EF⊥GO，利用等腰直角三角形的性质，可以得出∠OEG=∠EGO=∠OGE=∠GFO=45°，∠EGF=∠EGO+∠FGO=90°，用两种方式来表示△EGF的面积：

1

2

EG?FG=

1

2

EF?OG，EG和FG是下个大半圆的半径，设为R，得出R²=3×

3

2

=

9

2

，然后可求出中间圆O的内部非阴影部分的面积是2倍的（

1

4

大圆面积-△EGF的面积），这样阴影部分的面积就等于（中间小圆面积-中间圆O的内部非阴影部分的面积），即可得解．

解答：解：如下图，找出中间的圆与矩形相切的交点G、H，连接E、F，连接G、H，连接E、G，连接G、F，EF和GH的交点为O，
EO=FO=GO，GO⊥EF，利用等腰直角三角形的性质，可以得出∠OEG=∠EGO=∠OGE=∠GFO=45°，
∠EGF=∠EGO+∠FGO=90°，

用两种方式来表示△EGF的面积：

1

2

EG?FG=

1

2

EF?OG，EG和FG是下个大半圆的半径，设为R，得出R²=3×

3

2

=

9

2

，
中间圆O的内部非阴影部分的面积是：（

1

4

πR²-

1

2

EG?FG）×2=

9

4

π-

9

2

，
阴影部分的面积是：
π(

3

2

)2-（

9

4

π-

9

2

），
=

9

4

π-

9

4

π+

9

2

，
=

9

2

，
=4.5；
答：阴影部分的面积是4.5．

点评：此题考查了圆与组合图形，作辅助线，找出规律是解决此题的关键．