题目内容
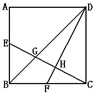正方形ABCD的面积是120平方厘米，E是AB的中点，F是BC的中点，四边形BGHF的面积是多少平方厘米？
解：因为E是AB的中点，F是BC的中点，
则S△BCE=S△DBF=S△DFC=
S正ABCD=×120=30平方厘米，
连接GF，F是BC的中点，则S△GBF=S△GFC，
又有对称性，得S△GBE=S△GBF=S△GFC=30÷3=10平方厘米，
由S△GHF：S△DGF=S△HFC：S△DFC=HF：DF，
得x：（30-10）=（10-x）：30，
30x=200-20x
50x=200，
x=4；
所以四边形BGHF的面积=S△GBF+S△GHF=10+4=14平方厘米．
答：四边形BGHF的面积是14平方厘米．
分析：因为E是AB的中点，F是BC的中点，则S△BCE=S△DBF=S△DFC=S正ABCD=×120=30平方厘米，连接GF，F是BC的中点，则S△GBF=S△GFC，
又有对称性，得S△GBE=S△GBF=S△GFC=30÷3=10平方厘米，由S△GHF：S△DGF=S△HFC：S△DFC=HF：DF，得x：（30-10）=（10-x）：30，
求出x的值，问题即可得解．
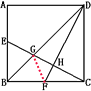
点评：解答此题的主要依据是：等底等高的三角形的面积相等，等高不等底的三角形的面积比就等于其对应底的比．
则S△BCE=S△DBF=S△DFC=
S正ABCD=×120=30平方厘米，连接GF，F是BC的中点，则S△GBF=S△GFC，
又有对称性，得S△GBE=S△GBF=S△GFC=30÷3=10平方厘米，
由S△GHF：S△DGF=S△HFC：S△DFC=HF：DF，
得x：（30-10）=（10-x）：30，
30x=200-20x
50x=200，
x=4；
所以四边形BGHF的面积=S△GBF+S△GHF=10+4=14平方厘米．
答：四边形BGHF的面积是14平方厘米．
分析：因为E是AB的中点，F是BC的中点，则S△BCE=S△DBF=S△DFC=
S正ABCD=×120=30平方厘米，连接GF，F是BC的中点，则S△GBF=S△GFC，又有对称性，得S△GBE=S△GBF=S△GFC=30÷3=10平方厘米，由S△GHF：S△DGF=S△HFC：S△DFC=HF：DF，得x：（30-10）=（10-x）：30，
求出x的值，问题即可得解．
点评：解答此题的主要依据是：等底等高的三角形的面积相等，等高不等底的三角形的面积比就等于其对应底的比．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
如图，正方形ABCD的面积为1，M是AD边上的中点，求图中阴影部分的面积．
E是正方形ABCD的边CD上的三等分点（如图），BE把正方形分成一个梯形和一个三角形．梯形的周长比三角形的周长大8厘米．正方形ABCD的面积是
[化整为零]．如图，正方形ABCD和正方形EFGH分别内接于同一个等腰直角三角形MBN（这里的内接指正方形的四个顶点全部在三角形的边上）．已知正方形ABCD的面积是72平方厘米，那么正方形EFGH的面积是多少平方厘米？
如图，已知图中阴部分的面积是57平方厘米，请求出这个正方形ABCD的面积．（π取3.14）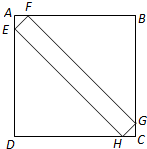
如图，正方形ABCD中，等腰直角三角形AEF的面积是1，长方形EFGH的面积是10，那么，正方形ABCD的面积是