题目内容
 长方形ABCD的长为9,宽为5,对角线AC被点W、X、Y和Z均分成5份.阴影部分的面积等于
长方形ABCD的长为9,宽为5,对角线AC被点W、X、Y和Z均分成5份.阴影部分的面积等于18
18
.分析:观察图形,根据“对角线AC被点W、X、Y和Z均分成5份”,利用高一定时,三角形的面积与底成正比例的性质可得:这四个阴影部分的三角形的面积都等于长方形的面积的一半的
,所以这四个阴影部分的三角形的面积之和就等于长方形的面积的一半的
,由此即可解答.
| 1 |
| 5 |
| 4 |
| 5 |
解答:解:因为对角线AC被点W、X、Y和Z均分成5份,
所以四个阴影部分的三角形的面积相等,都等于长方形的面积的一半的
,
所以这四个阴影部分的三角形的面积之和就等于长方形的面积的一半的
,
则9×5×
×
=18,
答:阴影部分的面积是18.
故答案为:18.
所以四个阴影部分的三角形的面积相等,都等于长方形的面积的一半的
| 1 |
| 5 |
所以这四个阴影部分的三角形的面积之和就等于长方形的面积的一半的
| 4 |
| 5 |
则9×5×
| 1 |
| 2 |
| 4 |
| 5 |
答:阴影部分的面积是18.
故答案为:18.
点评:此题考查了高一定时,三角形的面积与底成正比例的性质以及长方形的对角线把长方形分成两个相等的三角形的性质的综合应用.

练习册系列答案
相关题目
 如图所示,长方形ABCD的长为25,宽为15.四对平行线截长方形各边所得的线段的长已在图上标出,且横向的两组平行线都与BC平行.求阴影部分的面积.
如图所示,长方形ABCD的长为25,宽为15.四对平行线截长方形各边所得的线段的长已在图上标出,且横向的两组平行线都与BC平行.求阴影部分的面积.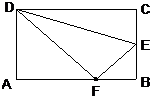 如图.长方形ABCD的长为6,宽为4,E是BC的中点.能否在线段AB上找一点F,使得△DEF的面积为13?若能,请说出F点的具体位置;若不能,请说明理由.
如图.长方形ABCD的长为6,宽为4,E是BC的中点.能否在线段AB上找一点F,使得△DEF的面积为13?若能,请说出F点的具体位置;若不能,请说明理由. 如右图,长方形ABCD的长为6厘米,宽为2厘米.经过点A做一条线段AE把长方形分成两部分,一部分是直角三角形,另一部分是梯形.如果梯形的面积是直角三角形面积的3倍,则,梯形的周长与直角三角形周长的差是
如右图,长方形ABCD的长为6厘米,宽为2厘米.经过点A做一条线段AE把长方形分成两部分,一部分是直角三角形,另一部分是梯形.如果梯形的面积是直角三角形面积的3倍,则,梯形的周长与直角三角形周长的差是 如图所示,长方形ABCD的长为25,宽为15.四对平行线截长方形各边所得的线段的长已在图上标出,且横向的两组平行线都与BC平行.求阴影部分的面积.
如图所示,长方形ABCD的长为25,宽为15.四对平行线截长方形各边所得的线段的长已在图上标出,且横向的两组平行线都与BC平行.求阴影部分的面积.