题目内容
 图中大长方形被分成四个小长方形,面积分别为12、24、36、48.请问:图中阴影部分的面积是多少?
图中大长方形被分成四个小长方形,面积分别为12、24、36、48.请问:图中阴影部分的面积是多少?
解:如图,阴影部分面积为:是 EF×AJ,
EF×AJ,
设大长方形的长为a,宽为b,
则EF= a-
a- a
a
=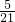 a,
a,
因此,阴影部分面积为 ×
×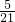 a×b,
a×b,
= ×
×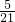 (a×b)
(a×b)
= ×(12+24+36+48)
×(12+24+36+48)
= ×120
×120
=
答:图中阴影部分的面积 .
.
故答案为: .
.
分析:如图,由于阴影部分是两个同底,高之和等于大长方形宽的三角形,其面积是 EF×AJ,我们可以设大长方形长AC=a,宽AJ=b,则EF的长为
EF×AJ,我们可以设大长方形长AC=a,宽AJ=b,则EF的长为 a-
a- a=
a=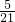 a,则阴影部分面积为
a,则阴影部分面积为 ×
×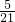 (a×b),由于a×b是大长方形的面积,其面积是四个小长方形面积之和,从而使问题得解.
(a×b),由于a×b是大长方形的面积,其面积是四个小长方形面积之和,从而使问题得解.
点评:EF是面积为48的长方形长的一部分,减去面积为12的长方形的长,由于没能告诉各小长方形及大长方形的长、宽,因此,只能用它们面积所占的分数来表示,得出用含有长度的代数式,进一步求解.此题难度较大.
 EF×AJ,
EF×AJ,设大长方形的长为a,宽为b,
则EF=
 a-
a- a
a=
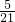 a,
a,因此,阴影部分面积为
 ×
×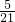 a×b,
a×b,=
 ×
×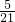 (a×b)
(a×b)=
 ×(12+24+36+48)
×(12+24+36+48)=
 ×120
×120=

答:图中阴影部分的面积
 .
.故答案为:
 .
.分析:如图,由于阴影部分是两个同底,高之和等于大长方形宽的三角形,其面积是
 EF×AJ,我们可以设大长方形长AC=a,宽AJ=b,则EF的长为
EF×AJ,我们可以设大长方形长AC=a,宽AJ=b,则EF的长为 a-
a- a=
a=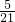 a,则阴影部分面积为
a,则阴影部分面积为 ×
×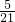 (a×b),由于a×b是大长方形的面积,其面积是四个小长方形面积之和,从而使问题得解.
(a×b),由于a×b是大长方形的面积,其面积是四个小长方形面积之和,从而使问题得解.点评:EF是面积为48的长方形长的一部分,减去面积为12的长方形的长,由于没能告诉各小长方形及大长方形的长、宽,因此,只能用它们面积所占的分数来表示,得出用含有长度的代数式,进一步求解.此题难度较大.

练习册系列答案
相关题目
 图中大长方形被分成四个小长方形,面积分别为12、24、36、48.请问:图中阴影部分的面积是多少?
图中大长方形被分成四个小长方形,面积分别为12、24、36、48.请问:图中阴影部分的面积是多少?