题目内容
 三角形BCD的面积为36玉方厘米,BD:OD=4:1,求梯形ABCD的面积?
三角形BCD的面积为36玉方厘米,BD:OD=4:1,求梯形ABCD的面积?分析:在梯形中,不难得出三角形AOB和三角形COD的面积相等,因为三角形BCD的面积为36玉方厘米,BD:OD=4:1,先根据高一定时,三角形的面积与底成正比例的性质求出三角形COD的面积,即可得出三角形AOB的面积;再根据BD:OD=4:1,求出三角形ABD的面积,再把这两部分的面积之和加起来,即可得出梯形得到面积.
解答:解:在梯形中,不难得出三角形AOB和三角形COD的面积相等,
因为三角形BCD的面积为36玉方厘米,BD:OD=4:1,
所以三角形COD的面积=
×三角形BCD的面积=
×36=9(平方厘米),
即三角形AOB的面积也是9平方厘米,
又因为BD:OD=4:1,所以BD=
BO,
所以三角形ABD的面积=
×三角形ABO的面积=9×
=12(平方厘米),
所以梯形的面积是:12+36=48(平方厘米),
答:梯形的面积是48平方厘米.
因为三角形BCD的面积为36玉方厘米,BD:OD=4:1,
所以三角形COD的面积=
| 1 |
| 4 |
| 1 |
| 4 |
即三角形AOB的面积也是9平方厘米,
又因为BD:OD=4:1,所以BD=
| 4 |
| 3 |
所以三角形ABD的面积=
| 4 |
| 3 |
| 4 |
| 3 |
所以梯形的面积是:12+36=48(平方厘米),
答:梯形的面积是48平方厘米.
点评:此题考查高一定时,三角形的面积与底成正比例的性质的应用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图中,六边形ABCDEF的面积是2010平方厘米.已知△ABC,△BCD,△CDE,△DEF,△EFA,△FAB的面积都等于335平方厘米,6个阴影三角形面积之和为670平方厘米.求六边形A1B1C1D1E1F1的面积.
如图中,六边形ABCDEF的面积是2010平方厘米.已知△ABC,△BCD,△CDE,△DEF,△EFA,△FAB的面积都等于335平方厘米,6个阴影三角形面积之和为670平方厘米.求六边形A1B1C1D1E1F1的面积.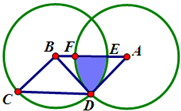 (2012?武汉模拟)如图,两个半径相等的圆A和圆B相交,三角形BCD是等腰直角三角形,其面积为60cm2,四边形ABCD是平行四边形,求图中阴影部分的面积.(π取3.14)
(2012?武汉模拟)如图,两个半径相等的圆A和圆B相交,三角形BCD是等腰直角三角形,其面积为60cm2,四边形ABCD是平行四边形,求图中阴影部分的面积.(π取3.14)