题目内容
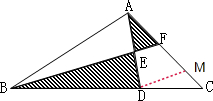
如图:阴影部分的面积是4平方厘米,AE=ED,BD=2DC,则三角形ABC面积为 平方厘米.


考点:三角形面积与底的正比关系
专题:平面图形的认识与计算
分析:如图,过D作DM∥BF交AC于M,因为AE=DE,所以△ABE的面积与△DBE的面积相等,所以阴影部分的面积为△DBE的面积+△AEF的面积,即三角形AFB的面积,由DM∥BF知道△DMC∽△CBF,所以CM:CF=CD:CB=1:3,即FM=
CF,因为EF是△ADM的中位线,AF=MF,所以AF=
AC,由此即可求出三角形ABC的面积,即阴影部分的面积.
| 2 |
| 3 |
| 2 |
| 5 |

解答:
解:过D作DM∥BF交AC于M(如图),
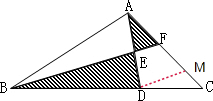
因为AE=DE,
所以△ABE的面积与△DBE的面积相等,
所以阴影部分的面积为△DBE的面积+△AEF的面积;
因为DM∥BF
所以△DMC∽△CBF,
因为BD=2DC,
所以:DC:BC=1:(1+2)=1:3,
所以CM:CF=CD:CB=1:3
即FM=
CF;
又因为AE=ED,EF∥DM,
所以EF是△ADM的中位线,
所以AF=MF,
所以AF=
AC;
所以△ABC的面积4÷
=10(平方厘米)
答:三角形ABC面积为10平方厘米.
故答案为:10.

因为AE=DE,
所以△ABE的面积与△DBE的面积相等,
所以阴影部分的面积为△DBE的面积+△AEF的面积;
因为DM∥BF
所以△DMC∽△CBF,
因为BD=2DC,
所以:DC:BC=1:(1+2)=1:3,
所以CM:CF=CD:CB=1:3
即FM=
| 2 |
| 3 |
又因为AE=ED,EF∥DM,
所以EF是△ADM的中位线,
所以AF=MF,
所以AF=
| 2 |
| 5 |
所以△ABC的面积4÷
| 2 |
| 5 |
答:三角形ABC面积为10平方厘米.
故答案为:10.
点评:本题也可以这样做:
如图,连接FD
 因为E是AD的中点,所以S△AEF=S△DEF,S△ABE=S△BDE.
因为E是AD的中点,所以S△AEF=S△DEF,S△ABE=S△BDE.
那么阴影部分=S△ABF=S△BDF=2S△CDF,
阴影部分=
S△ABC,
4÷
=10(平方厘米).
如图,连接FD
 因为E是AD的中点,所以S△AEF=S△DEF,S△ABE=S△BDE.
因为E是AD的中点,所以S△AEF=S△DEF,S△ABE=S△BDE.那么阴影部分=S△ABF=S△BDF=2S△CDF,
阴影部分=
| 2 |
| 5 |
4÷
| 2 |
| 5 |

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
4点钟后,从时针与分针第一次成90°角,到时针与分针第二次成90°角,共经过( )分钟.(答案四舍五入到整数)
| A、60 | B、30 | C、40 | D、33 |
现有1分,2分和5分的硬币各四枚,用其中的一些硬币支付2角3分钱,一共有多少种不同的支付方法?( )
| A、4 | B、5 | C、10 | D、8 |
 如图,三角形ABC中,AD=2BD,AD=EC,BC=18,三角形AFC的面积和四边形DBEF的面积相等,那么AB的长度是多少?
如图,三角形ABC中,AD=2BD,AD=EC,BC=18,三角形AFC的面积和四边形DBEF的面积相等,那么AB的长度是多少? 如图,在三角形ABC中,已知AE=EC,BD=
如图,在三角形ABC中,已知AE=EC,BD= 如图,P,Q分别是正方形ABCD的边AD和对角线 AC上的点,且PD:AP=4:1,QC:AQ=2:3,如果正方形ABCD的面积为25,那么三角形PBQ的面积是
如图,P,Q分别是正方形ABCD的边AD和对角线 AC上的点,且PD:AP=4:1,QC:AQ=2:3,如果正方形ABCD的面积为25,那么三角形PBQ的面积是 在一项射箭比赛中,规定每位运动员能射3支箭,射中了哪一环就得到哪一环上相应的分数,没有射中就不得分.这位运动员用3只支箭刚好射得50分的方式一共有
在一项射箭比赛中,规定每位运动员能射3支箭,射中了哪一环就得到哪一环上相应的分数,没有射中就不得分.这位运动员用3只支箭刚好射得50分的方式一共有 如图,灰太狼从A出发,不断往返于AB之间,懒羊羊从C出发按C-E-F-D围绕矩形不断行走.已知AC=80米,CD=EF=120米,CE=DF=30米,BD=100米,灰太狼的速度是5米/秒,懒羊羊的速度是4米/秒,灰太狼从背后第一次追上懒羊羊需要多少秒?
如图,灰太狼从A出发,不断往返于AB之间,懒羊羊从C出发按C-E-F-D围绕矩形不断行走.已知AC=80米,CD=EF=120米,CE=DF=30米,BD=100米,灰太狼的速度是5米/秒,懒羊羊的速度是4米/秒,灰太狼从背后第一次追上懒羊羊需要多少秒?