题目内容
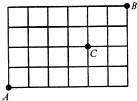如图，某城市的街道由5条东西与7条南北向马路组成．现在要从西南角的A处沿最短路线走到东北角的B处，由于修路十字路口C不能通过，那么共有多少种不同走法？分析：利用逐步分析点的路线，列出表格，求得数据即可解决问题．
解答：解：用标数法可以求出一共有120种走法．
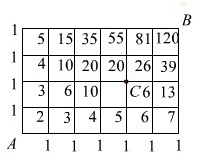
答：共有120种不同走法．
答：共有120种不同走法．
点评：本题从每个交叉点得出有2条路可走是关键，然后利用标数法得出共有的走法就比较容易了，注意C不能通过．
练习册系列答案
相关题目
如图，某城市的街道由5条东西与7条南北向马路组成．现在要从西南角的A处沿最短路线走到东北角的B处，由于修路十字路口C不能通过，那么共有多少种不同走法？
如图，某城市的街道由5条东西向马路和7条南北向马路组成，现在要从西南角的A处沿最短路线走到东北角的B处，有
如图所示，某城市的街道图，若从A走到B（只能由北向南，由西向东）则共有