题目内容
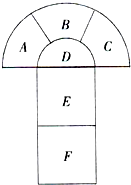 如图是一个变形的红十字一共分为六块区域.现在要用n种颜色对其染色,要求相邻的两块区域(有公共边的两块区域称为相邻)染成不同的颜色.如果颜色能反复使用,那么一共有
如图是一个变形的红十字一共分为六块区域.现在要用n种颜色对其染色,要求相邻的两块区域(有公共边的两块区域称为相邻)染成不同的颜色.如果颜色能反复使用,那么一共有n(n-1)3(n-2)2
n(n-1)3(n-2)2
种不同的染色方法(用n表示).分析:由图知,第一步假设A的n种,那么B就有n-1种,C和D就有(n-2)×(n-3)+1×(n-2)种,然后再分情况讨论C与A相同和不相同的两种情况,再确定E和F的种数,最后进行计算总共有多少种不同的方法.
解答:解:由图知,
第一步A:n,
第二步B:n-1,
第三步C、D:(n-2)×(n-3)+1×(n-2),
因为C可以和A相同,也可以和A不相同,C是否与A相同直接影响D,
第一类C与A相同:C:1,D:n-2,
第二类C与A不相同:C:n-2,D:n-3,
第四步E:n-1,
第五步F:n-1,
n×(n-1)×[(n-2)×(n-3)+1×(n-2)]×(n-1)×(n-1),
=n(n-1)3(n-2)2;
故答案为:n(n-1)3(n-2)2.
第一步A:n,
第二步B:n-1,
第三步C、D:(n-2)×(n-3)+1×(n-2),
因为C可以和A相同,也可以和A不相同,C是否与A相同直接影响D,
第一类C与A相同:C:1,D:n-2,
第二类C与A不相同:C:n-2,D:n-3,
第四步E:n-1,
第五步F:n-1,
n×(n-1)×[(n-2)×(n-3)+1×(n-2)]×(n-1)×(n-1),
=n(n-1)3(n-2)2;
故答案为:n(n-1)3(n-2)2.
点评:此题考查了染色问题,关键是在确定C与A相同和C与A不相同时要分两种情况进行讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图是一个游乐园的平面图.
如图是一个游乐园的平面图.

