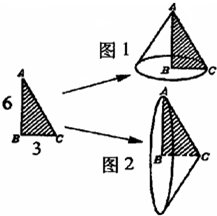
题目内容
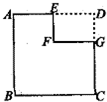 如图,从正方形ABCD上截去长方形DEFG,其中AB=1厘米,DE=
如图,从正方形ABCD上截去长方形DEFG,其中AB=1厘米,DE=| 1 |
| 2 |
| 1 |
| 3 |
| 11 |
| 3 |
| 11 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
分析:正方形以一边为轴,旋转一周得到的立体图形是一个圆柱,根据题干,将ABCGFE以GC边为轴旋转一周,这里可以把图中的图形分成两部分来看:①下面的长方形旋转一周得到的是一个底面半径为1厘米,高为1-
=
厘米的圆柱;②上面长方形旋转一周得到的是一个底面半径为
厘米,高为
厘米的圆柱;
(1)这个立体图形的表面积就是这下面大圆柱的表面积与上面小圆柱的侧面积之和;(图形中有重合的面)根据圆柱的表面积和体积公式即可解决问题.
(2)体积就是这两个圆柱的体积之和.
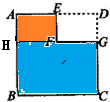
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(1)这个立体图形的表面积就是这下面大圆柱的表面积与上面小圆柱的侧面积之和;(图形中有重合的面)根据圆柱的表面积和体积公式即可解决问题.
(2)体积就是这两个圆柱的体积之和.

解答:解:(1)根据题干分析可得这个组合立体图形的表面积为:
π×12×2+2×π×1×
+2×π×
×
,
=2π+
π+
π,
=
π(平方厘米);
(2)体积为:
π×12×
+π×(
)2×
,
=
π+
π,
=
π(立方厘米);
答:所得几何体的表面积是
π平方厘米,体积是
π立方厘米.
故答案为:
π;
π.
π×12×2+2×π×1×
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
=2π+
| 4 |
| 3 |
| 1 |
| 3 |
=
| 11 |
| 3 |
(2)体积为:
π×12×
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
=
| 2 |
| 3 |
| 1 |
| 12 |
=
| 3 |
| 4 |
答:所得几何体的表面积是
| 11 |
| 3 |
| 3 |
| 4 |
故答案为:
| 11 |
| 3 |
| 3 |
| 4 |
点评:抓住题干得出旋转后的图形是两个圆柱是解决本题的关键,解题时要注意重合部分的面积.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 如图,正△ABC的边长是100米,BCDE是正方形,甲从A出发,沿正△ABC逆时针跑步,速度是4米/秒;乙从B同时出发,沿正方形逆时针跑步,速度是5米/秒.则甲、乙出发后
如图,正△ABC的边长是100米,BCDE是正方形,甲从A出发,沿正△ABC逆时针跑步,速度是4米/秒;乙从B同时出发,沿正方形逆时针跑步,速度是5米/秒.则甲、乙出发后