题目内容
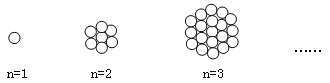
【题目】如图,当n=1时,图中有1个圆;当n=2时,图中有7个圆;当n=3时,图中有19个圆;…,按此规律,当n=5时,图中有 个圆.
【答案】61
【解析】所构成的图形是轴对称图形,沿中间的一列分开,两边对称,最左边的一行是n个圆,后面每一列比前面的每一列多一个,直到中间的一列,中间的一排是2n﹣1个.中间的后面的每排依次减少.
解:最左边的一列是n,第二列是n+1,第三列是n+2,…,第n列是2n﹣1;
第n列以后,各列的个数分别是2n﹣2,2n﹣3…,n.
则第n个图形的圆的个数是:
n+(n+1)+…(2n﹣1)+(2n﹣2)+(2n﹣3)+…+n
=2[n+(n+1)+(n+2)+…+(2n﹣2)]+(2n﹣1)
=(n﹣1)[n+(2n﹣2)]+(2n﹣1)
=3n2﹣3n+1.
所以当n=5时,图中有圆:3×52﹣3×5+1,
=3×25﹣15+1,
=75﹣15+1,
=61(个),
答:当n=5时,图中有圆61个.
故答案是:61.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目