题目内容
有三个数字，用他们可以组成六个不同的三位数的和是3330，其中最大的三位数是多少？
分析：设这三个数字为A，B，C．则则组成的6个不同的三位数为ABC、ACB、BAC、BCA、CAB、CBA．根据数位知识，它们相为的和可表示为：100A+10B+C+100A+10C+B+100B+10C+A+100B+10A+C+100C+10+B+100C+10+A=2×（A+B+C）+20×A+B+C）+200×（A+B+C）=3330，解得：（A+B+C）为15．然后列举出相加和为10的三个数后，即能求得其中最大的三位数是多少．
解答：解：设这三个数字为A，B，C．
组成的6个不同的三位数为ABC、ACB、BAC、BCA、CAB、CBA，则：
100A+10B+C+100A+10C+B+100B+10C+A+100B+10A+C+100C+10+B+100C+10+A
=2×（A+B+C）+20×A+B+C）+200×（A+B+C）
=3330；
即：（A+B+C）+10×（A+B+C）+100×（A+B+C）=1665；
解得：（A+B+C）=15
则A、B、C所有可能的组合为：1 6 8；1 5 9；2 6 7；2 5 8；2 4 9；3 5 7；3 4 8；4 5 6；
其中能组成的最大的三位数为：951．
组成的6个不同的三位数为ABC、ACB、BAC、BCA、CAB、CBA，则：
100A+10B+C+100A+10C+B+100B+10C+A+100B+10A+C+100C+10+B+100C+10+A
=2×（A+B+C）+20×A+B+C）+200×（A+B+C）
=3330；
即：（A+B+C）+10×（A+B+C）+100×（A+B+C）=1665；
解得：（A+B+C）=15
则A、B、C所有可能的组合为：1 6 8；1 5 9；2 6 7；2 5 8；2 4 9；3 5 7；3 4 8；4 5 6；
其中能组成的最大的三位数为：951．
点评：根据已知条件及数位知识列出等量关系式进行分析，得出这三个数的和是多少是完成本题的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
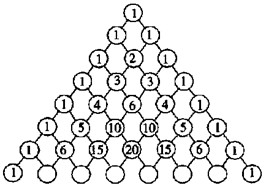如图是在研究杨辉三角问题时的系数的规律图．第一层只有一个数字1；第二层有两个数字1，1；第三层有三个数字1，2，l，…．观察图中的规律，试回答：