题目内容
在下面一列数中，从第二个数开始，每个数都比它前面相邻的数大7，8，15，22，29，36，43，…．
它们前n-1个数相乘的积的末尾0的个数比前n个数相乘的积的末尾0的个数少3个，求n的最小值．
它们前n-1个数相乘的积的末尾0的个数比前n个数相乘的积的末尾0的个数少3个，求n的最小值．
分析：观察这列数可知每个数除以7余数为1，由题意知若使n最小，则第n个数必须含有3个5的因子，这样由5的因子数少于2因子数知前n个相乘方会比前n-1个多3个0．所以第n个数可写成5×5×k的形式，即为125k（k为自然数）且125k除以7余数为1，这样最小的k值为6．进而解决问题．
解答：解：由题意知若使n最小，则第n个数必须含有3个5的因子，这样由5的因子数少于2因子数知前n个相乘方会比前n-1个多3个0．
所以第n个数可写成5×5×k的形式，即为125k（k为自然数）且125k除以7余数为1，这样最小的k值为6．
即第n个数为7n+1=750．此时再根据第n个数又可表示为7n+1，可得n=107．
答：n的最小值为107．
所以第n个数可写成5×5×k的形式，即为125k（k为自然数）且125k除以7余数为1，这样最小的k值为6．
即第n个数为7n+1=750．此时再根据第n个数又可表示为7n+1，可得n=107．
答：n的最小值为107．
点评：此题解答的关键在于根据题意，表示出第n个数，写成5×5×k的形式．
练习册系列答案
相关题目
表示其中的第n项，那么
。
及
。又如向日葵花序中小花或籽粒的排列，顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
)，34∶55(
)，89∶144(
)，在一些大型样本中，这个比值甚至为144∶233(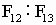
)。同样，生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数，一般总是落在斐波那契数列3，5，8和13相邻的两数中。
表示其中的第n项，那么
。
及
。又如向日葵花序中小花或籽粒的排列，顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
)，34∶55(
)，89∶144(
)，在一些大型样本中，这个比值甚至为144∶233(
)。同样，生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数，一般总是落在斐波那契数列3，5，8和13相邻的两数中。