题目内容
ABCD是平行四边形，其面积是20平方厘米，求尖朝上的3个小三角形的面积．
分析：从图中看出平行四边形ABCD被分成6个高相等的三角形，由此根据三角形的面积公式S=ah÷2，与平行四边形的面积公式S=ah，得出在高相等时，面积的比与底的比的关系，据此解答．
解答：解：因为AE=
AB，
所以尖朝上的3个小三角形的面积是：3×AE×h÷2=AB×h÷2=20÷2=10（平方厘米）
答：尖朝上的3个小三角形的面积10平方厘米．
| 1 |
| 3 |
所以尖朝上的3个小三角形的面积是：3×AE×h÷2=AB×h÷2=20÷2=10（平方厘米）
答：尖朝上的3个小三角形的面积10平方厘米．
点评：本题也可以根据平行四边形ABCD被分成6个高相等的三角形，尖朝上的3个小三角形的面积和尖朝下的3个小三角形的面积相等，直接用平行四边形的面积除以2即可．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，四边形ABCD是平行四边形，E在边BC上，三角形ABE的面积是78平方厘米，求阴影面积．
四边形ABCD是平行四边形，AE=3，ED=5，空白部分的三角形面积是10，球阴影部分的面积．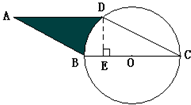
如图圆的直径BC=8厘米，ABCD是平行四边形，线段AB=7厘米，DE=3.5厘米，∠BCD=30度，求阴影部分的周长和面积．（ π取3）