题目内容

1+2+3+…+1995+1996+2001的和是奇数．
√
√
．
分析：先根据高斯求和公式求出1～1996这1996个自然数的和：（1+1996）×1996÷2=1993006；然后把这个和与2001相加是：1993006+2001=1995007，个位数字是奇数，所以1+2+3+…+1995+1996+2001的和是奇数；据此解答．
解答：解：1+2+3+…+1995+1996+2001，
=（1+1996）×1996÷2+2001，
=1993006+2001，
=1995007，
个位数字是奇数，所以1+2+3+…+1995+1996+2001的和是奇数．
故答案为：√．
点评：本题考查了高斯求和公式的实际应用，知识点是：和=（首项+末项）×项数÷2；
方法二：还可根据1996个相邻的自然数相加的和是偶数，又因为2001是奇数，根据偶数+奇数=奇数可得：1+2+3+…+1995+1996+2001的和是奇数，问题得解．
练习册系列答案
相关题目
观察下面几个算式，你发现了什么？
1+2+1=4
1+2+3+2+1=9
1+2+3+4+3+2+1=16
1+2+3+4+5+4+3+2+1=25
我发现了：
从1开始连续加到几，再按倒序加到1，计算的结果是几乘几，用算式表示为：1+2+3+…+（n-1）+n+（n-1）+…+3+2+1=n×n
从1开始连续加到几，再按倒序加到1，计算的结果是几乘几，用算式表示为：1+2+3+…+（n-1）+n+（n-1）+…+3+2+1=n×n
．
利用这个规律，请你很快地说出下面各题的得数：
1+2+3+…+9+10+9+…+3+2+1=
100
100
；
1+2+3+…+19+20+19+…+3+2+1=
400
400
；
1+2+3+…+29+30+29+…+3+2+1=
900
900
．
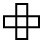（2008?金坛市）如果用去框右面这个数表里的数，每次框出5个数，一共可以框出
15
15
个不同的和．如果框出的5个数的和是130，这个5个数中最小的一个是
19
19
．
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31 32 33 34 35
在下面的数字方阵中有400个数，这400个数的和等于
8000
8000
．
1 2 3 … … 19 20
2 3 4 … … 20 21
3 4 5 … … 21 22
… … … … … … …
19 20 21 … … 37 38
20 21 22 … … 38 39
在2的倍数上画▲，在5的倍数上画○．
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
2和5的公倍数有
 
，最小的公倍数是
 
．
用“○”画出下表中所有6的倍数．
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 39
31 32 33 34 35 36 37 38 39 40

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网