题目内容
计算:
(1)6+11+16+…+501
(2)1+5+9+13+…+1989+1993.
(1)6+11+16+…+501
(2)1+5+9+13+…+1989+1993.
分析:利用等差数列的通项公式an=a1+(n-1)d,得出n=(an-a1)÷d+1,求出项数n,再根据等差数列的求和公式Sn=(a1+an)×n÷2,求出和.
解答:解:(1)(501-6)÷(11-6)+1,
=495÷5+1,
=100,
(6+501)×100÷2,
=507×100÷2,
=25350;
(2)(1993-1)÷(5-1)+1,
=1992÷4+1,
=498+1,
=499,
(1+1993)×499÷2,
=1994×499÷2,
=995006÷2,
=497503.
=495÷5+1,
=100,
(6+501)×100÷2,
=507×100÷2,
=25350;
(2)(1993-1)÷(5-1)+1,
=1992÷4+1,
=498+1,
=499,
(1+1993)×499÷2,
=1994×499÷2,
=995006÷2,
=497503.
点评:本题主要是灵活利用等差数列的通项公式an=a1+(n-1)d和求和公式Sn=(a1+an)×n÷2 解决问题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 ×3574+642.9×66-3÷
×3574+642.9×66-3÷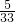

 +5
+5 +7
+7 +9
+9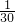 +11
+11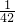
 X-
X- =
= X-
X- .
.