题目内容
 如图,BE=EF=FC,GA=AH=HC,三角形ABC的面积为6平方厘米,三角形GEC的面积是多少平方厘米?
如图,BE=EF=FC,GA=AH=HC,三角形ABC的面积为6平方厘米,三角形GEC的面积是多少平方厘米?分析:如图:连接接GB,AE,根据BE=EF=FC,知道EC=
BC,所以三角形AEC的面积是三角形ABC面积的
,即6×
=4平方厘米,由BE=EF=FC,GA=AH=HC,知道AE平行BG,三角形GAE和三角形BAE有同底AE,等高(平行线间的垂直线段相等),所以三角形GAE的面积=三角形BAE的面积=
×三角形ABC的面积=2平方厘米,由此即可求出三角形GEC的面积.

| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |

解答:解:连接接GB,AE,因为BE=EF=FC,
所以EC=
BC,所以三角形AEC的面积是三角形ABC面积的
,即6×23=4(平方厘米),
因为BE=EF=FC,GA=AH=HC,所以AE平行BG,三角形GAE和三角形BAE有同底AE,等高(平行线间的垂直线段相等),
所以三角形GAE的面积=三角形BAE的面积=
×三角形ABC的面积=
×6=2(平方厘米),
三角形GEC的面积=三角形AEC的面积+三角形GAE的面积:2+4=6(平方厘米),
答:三角形GEC的面积是6平方厘米.
所以EC=
| 2 |
| 3 |
| 2 |
| 3 |
因为BE=EF=FC,GA=AH=HC,所以AE平行BG,三角形GAE和三角形BAE有同底AE,等高(平行线间的垂直线段相等),
所以三角形GAE的面积=三角形BAE的面积=
| 1 |
| 3 |
| 1 |
| 3 |
三角形GEC的面积=三角形AEC的面积+三角形GAE的面积:2+4=6(平方厘米),
答:三角形GEC的面积是6平方厘米.
点评:本题主要考查了三角形的高一定时,底与面积的正比关系.

练习册系列答案
相关题目
 如图,在三角形ABC中,BE=EF=FC,ED=2DA,求阴影部分的面积是三角形ABC面积的几分之几?
如图,在三角形ABC中,BE=EF=FC,ED=2DA,求阴影部分的面积是三角形ABC面积的几分之几? (2013?北京模拟)如图,在△ABC中,AD=
(2013?北京模拟)如图,在△ABC中,AD= 如图,∠ABE=∠DCF=90°,AB=3,DC=5,BC=6,BE=EF=FC,AF交DE于G.则三角形DFG与三角形AGE面积的和为
如图,∠ABE=∠DCF=90°,AB=3,DC=5,BC=6,BE=EF=FC,AF交DE于G.则三角形DFG与三角形AGE面积的和为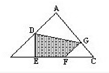 如图,在△ABC中,AD=
如图,在△ABC中,AD=