题目内容
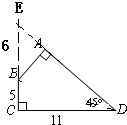
 如图,四边形ABCD两条边CD=11,BC=5,∠A和∠C是直角,∠D是45°,这个四边形的面积是
如图,四边形ABCD两条边CD=11,BC=5,∠A和∠C是直角,∠D是45°,这个四边形的面积是考点:组合图形的面积
专题:平面图形的认识与计算
分析:如下图,延长CB和DA交于点E,因为∠D=45,∠C是直角,所以△DCE是等腰直角三角形,EC=CD=11,BE=CE-CB=11-5=6,△ABE是等腰直角三角形,BE边上的高=BE的
=3,所求四边形的面积=△DCE的面积-△ABE的面积,据此得解.
| 1 |
| 2 |
解答:
解:如图,延长CB和DA交于点E,
×11×11-
×(11-5)×
=
×121-
×6×3
=60.5-9
=51.5
答:这个四边形的面积是51.5.
故答案为:51.5.

| 1 |
| 2 |
| 1 |
| 2 |
| 11-5 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=60.5-9
=51.5
答:这个四边形的面积是51.5.
故答案为:51.5.
点评:分析图形,根据图形特点进行割补,寻求问题突破点.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 如图,将正方形纸片由下往上对折,再由左向右对折,称为完成一次操作.按上述方法完成4次操作以后,请问:
如图,将正方形纸片由下往上对折,再由左向右对折,称为完成一次操作.按上述方法完成4次操作以后,请问: 如图,阴影部分是一个斜置的正方形,E、F是BC边上的三等分点,已知阴影面积是2,那么正方形ABCD的面积是
如图,阴影部分是一个斜置的正方形,E、F是BC边上的三等分点,已知阴影面积是2,那么正方形ABCD的面积是