Question

把1～11这11个数分别填入如下图11个○内，使每条虚线上三个○内数的和相等，一共有几种不同的和？

Answer 1

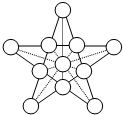
分析：假设中间○内填入的数是a，每条虚线上三个○内数的和是k，则有1+2+3+4+5+6+7+8+9+10+11+4a=5k，66+4a=5k：
当a=1时，k=（66+4）÷5=14；
当a=2、3、4、5、时，k不是整数，无解；
当a=6时，k=（66+24）÷5=18；
当a=7、8、9、10时，k不是整数，无解；
当a=11时，k=（66+44）÷5=22；
即可得解．一共有3种不同的和．

解答：解：把1～11这11个数分别填入如下图11个○内，使每条虚线上三个○内数的和相等，一共有3种不同的和.14、18、22，如下图所示：

点评：此题考查了凑数谜．根据已知，列出含两个未知数的等式，逐个实验，得出结论．这就是凑数谜的一种解题方法．