题目内容
 用写有+1和-1的长方块放在10×n方格中,使得每一列和每一行的数的乘积都是正的,n的最小值是多少?
用写有+1和-1的长方块放在10×n方格中,使得每一列和每一行的数的乘积都是正的,n的最小值是多少?分析:由题意可得:每一列,每一行的-1的个数都是偶数个,所以,整个方格中的-1的个数是偶数个,而-1的个数就是长方块的个数.所以可设有2m个长方块.每个长方块占2个格.当长方块放满的时候,10n=4m,5n=2m,所以n=2k,m=5k,k=1,2,3,…然后从最小的2开始进行讨论,得出符合题意的答案.
解答:解:每一列,每一行的-1的个数都是偶数个,所以,整个方格中的-1的个数是偶数个,而-1的个数就是长方块的个数.所以可设有2m个长方块.每个长方块占2个格.
当长方块放满的时候,10n=4m,5n=2m,所以n=2k,m=5k,k=1,2,3,…
最小的n=2,但是,若n=2,m=5,长方块不能水平放置,竖直放置5个长方块,每一列恰好5个-1,不可能满足要求的情况.
n=4,m=10,如图.每个长方块都是水平放置+1,在左边,-1在右边即可.
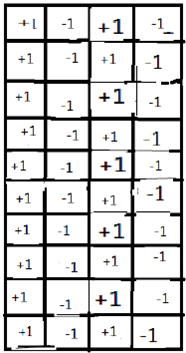
答:n的最小值是4.
当长方块放满的时候,10n=4m,5n=2m,所以n=2k,m=5k,k=1,2,3,…
最小的n=2,但是,若n=2,m=5,长方块不能水平放置,竖直放置5个长方块,每一列恰好5个-1,不可能满足要求的情况.
n=4,m=10,如图.每个长方块都是水平放置+1,在左边,-1在右边即可.

答:n的最小值是4.
点评:由题意得出:每一列,每一行的-1的个数都是偶数个,所以,整个方格中的-1的个数是偶数个,而-1的个数就是长方块的个数,是解题关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目


 526
526 321
321 ,平均插在4个花瓶里,可以插
,平均插在4个花瓶里,可以插