Question

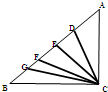（2011?汉阳区）如图△ABC中，点D、E、F、G为AB边上四点，且

AD

AB

=

DE

DB

=

EF

EB

=

FG

FB

=

1

3

，△ABC的面积积是1，则△AGC的面积是

65

81

．

Answer 1

分析：因为

AD

AB

=

DE

DB

=

EF

EB

=

FG

FB

=

1

3

，根据高一定时，三角形的面积与底成正比例的性质，可得三角形BCG=

2

3

三角形BFC=

2

3

×

2

3

三角形BEC=

2

3

×

2

3

×

2

3

三角形BDC=

2

3

×

2

3

×

2

3

×

2

3

三角形ABC=

16

81

三角形ABC，因为三角形ABC的面积是1，由此求出三角形BGC的面积，根据三角形AGC的面积=三角形ABC的面积-三角形BGC的面积即可解答．

解答：解：因为

AD

AB

=

DE

DB

=

EF

EB

=

FG

FB

=

1

3

，
所以三角形BCG=

2

3

三角形BFC，
=

2

3

×

2

3

三角形BEC，
=

2

3

×

2

3

×

2

3

三角形BDC，
=

2

3

×

2

3

×

2

3

×

2

3

三角形ABC，
=

16

81

三角形ABC，
因为三角形ABC的面积是1，
所以三角形BCG=

16

81

×1=

16

81

，
所以三角形AGC=1-

16

81

=

65

81

．
答：三角形AGC的面积是

65

81

．

点评：此题考查了高一定时，三角形的面积与底成正比的关系的灵活应用．