Question

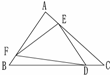如图，已知AE=

1

5

AC，CD=

1

4

BC，BF=

1

6

AB，那么，

三角形DEF的面积

三角形ABC的面积

=

61

120

．

Answer 1

分析：可以先求出边上的3个小三角形与S_△ABC的面积之间的关系：S_△BDF=S_△ABC×

3

4

×

1

6

=

1

8

S_△ABC，S_△CDE=S_△ABC×

1

4

×

4

5

=

1

5

S_△ABC，S_△AEF=S_△ABC×

1

5

×

5

6

=

1

6

S_△ABC，所以 S_△DEF=S_△ABC-S_△BDF-S_△CDE-S_△AEF=

61

120

S_△ABC，依此即可求解．

解答：解：S_△BDF=S_△ABC×

3

4

×

1

6

=

1

8

S_△ABC，
S_△CDE=S_△ABC×

1

4

×

4

5

=

1

5

S_△ABC，
S_△AEF=S_△ABC×

1

5

×

5

6

=

1

6

S_△ABC，
S_△DEF=S_△ABC-S_△BDF-S_△CDE-S_△AEF=

61

120

S_△ABC，

三角形DEF的面积

三角形ABC的面积

=

61

120

．
故答案为：

61

120

．

点评：考查了三角形面积与底的正比关系，得到边上的3个小三角形与S_△ABC的面积之间的关系是解题的难点，本题有一定的难度．