题目内容
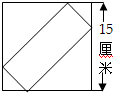 如图,正方形中套着一个长方形,正方形的边长是15厘米,长方形的四个角的顶点,恰好分别把正方形四条边都公成两段,其中长的一段是短的2倍.这个长方形的面积是多少?
如图,正方形中套着一个长方形,正方形的边长是15厘米,长方形的四个角的顶点,恰好分别把正方形四条边都公成两段,其中长的一段是短的2倍.这个长方形的面积是多少?分析:如图所示,由题意可知:三角形①、②、③、④应均为等腰直角三角形,且①和②组成1个边长为5厘米的正方形,③和④能组成1个边长为10厘米的正方形,用大正方形的面积分别减去这两个小正方形的面积,就是长方形的面积.


解答:解:由题意可得:AE=AH=CG=CF=
AD=
×15=5(厘米),
DH=DG=BF=BE=
AD=
×15=10(厘米),
所以长方形EFGH的面积是:
15×15-10×10-5×5,
=225-100-25,
=100(平方厘米);
答:长方形EFGH的面积是100平方厘米.
| 1 |
| 3 |
| 1 |
| 3 |
DH=DG=BF=BE=
| 2 |
| 3 |
| 2 |
| 3 |
所以长方形EFGH的面积是:
15×15-10×10-5×5,
=225-100-25,
=100(平方厘米);
答:长方形EFGH的面积是100平方厘米.
点评:解答此题的关键是:利用其他图形的面积和或差求出长方形的面积.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 如图,正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个顶点恰好分别把正方形的四条边分成两段,其中长的一段长度是短的2倍,这个长方形的面积是
如图,正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个顶点恰好分别把正方形的四条边分成两段,其中长的一段长度是短的2倍,这个长方形的面积是 (2012?杨浦区)如图,一个正方形中套着一个长方形,已知正方形的边长是16分米,长方形的四个角的顶点恰好把正方形四条边都分成两段,其中长的一段是短的3倍.阴影部分的面积是多少?
(2012?杨浦区)如图,一个正方形中套着一个长方形,已知正方形的边长是16分米,长方形的四个角的顶点恰好把正方形四条边都分成两段,其中长的一段是短的3倍.阴影部分的面积是多少? 如图,正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个顶点恰好分别把正方形的四条边分成两段,其中长的一段长度是短的2倍,这个长方形的面积是________.
如图,正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个顶点恰好分别把正方形的四条边分成两段,其中长的一段长度是短的2倍,这个长方形的面积是________. 如图,正方形中套着一个长方形,正方形的边长是15厘米,长方形的四个角的顶点,恰好分别把正方形四条边都公成两段,其中长的一段是短的2倍.这个长方形的面积是多少?
如图,正方形中套着一个长方形,正方形的边长是15厘米,长方形的四个角的顶点,恰好分别把正方形四条边都公成两段,其中长的一段是短的2倍.这个长方形的面积是多少?