题目内容
如图,AD= AB、FC=
AB、FC= AC、BE=
AC、BE= BC;如果三角形ABC中的阴影面积是19平方厘米,那么三角形ABC的面积是________平方厘米.
BC;如果三角形ABC中的阴影面积是19平方厘米,那么三角形ABC的面积是________平方厘米.
45.6
分析:根据三角形各个边的关系,可求出空白处的3个三角形的面积各占三角形ABC面积的几分之几,把三角形ABC看作单位“1”,用单位“1”减去空白部分三角形BED、三角形CDE、三角形ACD各占三角形ABC的份数,就可得到阴影部分占三角形ABC的份数,根据已知一个数占另一个数的几分之几,求另一个数是多少,可用除法进行计算.
解答:根据AD:AB=1:3,BE:BC=1:4,
那么三角形DBE的高为三角形ABC的 ,
,
底为三角形ABC的 ,
,
三角形BDE的面积为大三角形ABC的 ×
× =
= ;
;
同理可得:
三角形EFC的面积为大三角形ABC的 ×
× =
= ,
,
三角形AFD的面积为大三角形ABC的 ×
× =
= ;
;
则DEF的面积占三角形ABC的面积的比例为:
[1-( +
+ +
+ )=
)= ,
,
已知,三角形DEF的面积是19,
则大三角形ABC的面积:19÷ =45.6(平方厘米);
=45.6(平方厘米);
答:三角形ABC的面积是45.6平方厘米.
故答案为:45.6.
点评:解答此题的关键是分析出空白部分的各条边与三角形ABC各边的关系,再利用一个数是另一个数的几分之几的,求另一个数的知识点进行解答.
分析:根据三角形各个边的关系,可求出空白处的3个三角形的面积各占三角形ABC面积的几分之几,把三角形ABC看作单位“1”,用单位“1”减去空白部分三角形BED、三角形CDE、三角形ACD各占三角形ABC的份数,就可得到阴影部分占三角形ABC的份数,根据已知一个数占另一个数的几分之几,求另一个数是多少,可用除法进行计算.
解答:根据AD:AB=1:3,BE:BC=1:4,
那么三角形DBE的高为三角形ABC的
 ,
,底为三角形ABC的
 ,
,三角形BDE的面积为大三角形ABC的
 ×
× =
= ;
;同理可得:
三角形EFC的面积为大三角形ABC的
 ×
× =
= ,
,三角形AFD的面积为大三角形ABC的
 ×
× =
= ;
;则DEF的面积占三角形ABC的面积的比例为:
[1-(
 +
+ +
+ )=
)= ,
,已知,三角形DEF的面积是19,
则大三角形ABC的面积:19÷
 =45.6(平方厘米);
=45.6(平方厘米);答:三角形ABC的面积是45.6平方厘米.
故答案为:45.6.
点评:解答此题的关键是分析出空白部分的各条边与三角形ABC各边的关系,再利用一个数是另一个数的几分之几的,求另一个数的知识点进行解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
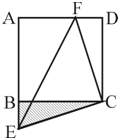 如图所示,设F为正方形ABCD边AD上一点,CE⊥CF交AB的延长线于E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为
如图所示,设F为正方形ABCD边AD上一点,CE⊥CF交AB的延长线于E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为 如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为
如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为

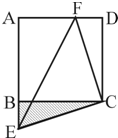 如图所示,设F为正方形ABCD边AD上一点,CE⊥CF交AB的延长线于E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为________.
如图所示,设F为正方形ABCD边AD上一点,CE⊥CF交AB的延长线于E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为________.