题目内容
8.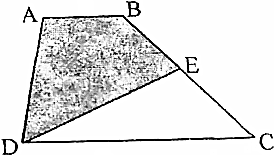 如图,梯形ABCD的上底是下底的$\frac{1}{3}$,E为腰上的中点,阴影部分的面积是15cm2,则梯形的面积是多少?
如图,梯形ABCD的上底是下底的$\frac{1}{3}$,E为腰上的中点,阴影部分的面积是15cm2,则梯形的面积是多少?
分析 设AB=x厘米,梯形ABCD的上底是下底的$\frac{1}{3}$,则DC=3x厘米;因为E为腰上的中点,所以梯形ABCD是△DEC的高的2倍,所以设△DEC的高为h厘米,则梯形ABCD的高为2h厘米,因而求出S△DCE:S梯形ABCD的值,再根据阴影部分的面积是15cm2,求出梯形面积即可.
解答 解:设AB=x厘米,梯形ABCD的上底是下底的$\frac{1}{3}$,则DC=3x厘米,
因为E为腰上的中点,所以梯形ABCD是△DEC的高的2倍,
所以设△DEC的高为h厘米,则梯形ABCD的高为2h厘米,
所以S△DCE:S梯形ABCD=($\frac{1}{2}$×3x×h):[$\frac{1}{2}$×(x+3x)×2h]=3:8,
又因为阴影部分的面积是15cm2,
所以梯形面积为:
15÷(1-$\frac{3}{8}$)
=15÷$\frac{5}{8}$
=24(平方分米).
答:梯形的面积是24平方分米.
点评 此题解答的关键在于根据已知条件求出S△DCE:S梯形ABCD的值,进而解决问题.

练习册系列答案
相关题目
19.计算398÷48时,我们可以把48看作( )来试商.
| A. | 40 | B. | 50 | C. | 45 |
20.用3厘米、4厘米、5厘米、5厘米的小棒中任选3根,能组成( )种不同的等腰三角形.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.口算.
| 170%+3= | 1÷5%= | 100×25%= | 1-3%= |
| 45÷30%= | 4÷80= | $\frac{3}{8}$-37.5%= | $\frac{3}{4}$÷75%×$\frac{3}{4}$= |
