题目内容
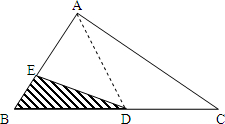
 如图中三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4,BE=2,EA=4,那么甲部分的面积是乙部分面积的几分之几?
如图中三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4,BE=2,EA=4,那么甲部分的面积是乙部分面积的几分之几?考点:三角形面积与底的正比关系
专题:几何的计算与计数专题
分析:要求阴影部分面积是空白部分面积的几分之几,就要推出阴影部分与空白部分面积的关系.如下图,连接AD,根据三角形底与面积的正比关系,先推出S阴影=
S△ADE,S△ADC=S△ABD;再根据△ADE与阴影的面积关系,即可得出问题的答案.
| 1 |
| 2 |
解答:
解:解:如图,连接AD,
因为E是AB的三等分点,所以S阴影=
S△ADE,S△ADC=S△ABD(等底等高);
又因为S△ABD=S△ADE+S阴影=S△ADE+
S△ADE=
S△ADE;
所以S△ADC=
S△ADE;
那么空白部分的面积为:
S△ADC+S△ADE=
S△ADE+S△ADE=
S△ADE;
由前面S阴影=
S△ADE,可知S△ADE=2×S阴影,
因此S△ADC+S△ADE=
×2×S阴影=5×S阴影,即S阴影=
×(S△ADC+S△ADE);
因此阴影部分面积是空白部分面积的
.

因为E是AB的三等分点,所以S阴影=
| 1 |
| 2 |
又因为S△ABD=S△ADE+S阴影=S△ADE+
| 1 |
| 2 |
| 3 |
| 2 |
所以S△ADC=
| 3 |
| 2 |
那么空白部分的面积为:
S△ADC+S△ADE=
| 3 |
| 2 |
| 5 |
| 2 |
由前面S阴影=
| 1 |
| 2 |
因此S△ADC+S△ADE=
| 5 |
| 2 |
| 1 |
| 5 |
因此阴影部分面积是空白部分面积的
| 1 |
| 5 |
点评:此题主要利用三角形的面积与底的正比关系,推出各三角形之间的面积关系,进而解决问题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目


 一张边长6厘米的正方形纸,沿着每一边的中点到邻边的中点连成一条线段,沿着每一条线段剪去4个角,你能求出剩下的面积吗?
一张边长6厘米的正方形纸,沿着每一边的中点到邻边的中点连成一条线段,沿着每一条线段剪去4个角,你能求出剩下的面积吗?