题目内容
 已知如图线段OC的长度是OA的3倍,三角形DOC的面积是18平方厘米,梯形ABCD的面积是
已知如图线段OC的长度是OA的3倍,三角形DOC的面积是18平方厘米,梯形ABCD的面积是96
96
平方厘米.分析:要求梯形ABCD的面积可以将它分成两部分来求,即:求出△ADC与△ABC的面积.
(1)△ADC的面积:因为线段OC的长度是OA的3倍,所以AC=
OC,所以△ADC的面积=
△DOC的面积=
×18=24平方厘米,
(2)△ABC的面积:梯形中△AOD与△BOC相似,AD:BC=OA:OC=1:3,因为△ACD与△ABC的底相同,所以△ACD与△ABC的面积比为1:3,由此可得△ABC的面积为:24×3=72平方厘米.
由上述计算即可得出梯形ABCD的面积.
(1)△ADC的面积:因为线段OC的长度是OA的3倍,所以AC=
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
(2)△ABC的面积:梯形中△AOD与△BOC相似,AD:BC=OA:OC=1:3,因为△ACD与△ABC的底相同,所以△ACD与△ABC的面积比为1:3,由此可得△ABC的面积为:24×3=72平方厘米.
由上述计算即可得出梯形ABCD的面积.
解答:解:根据题干可得:AC=
OC,,
△ADC的面积:
×18=24(平方厘米),
AD:BC=OA:OC=1:3,因为△ACD与△ABC的底相同,所以△ACD与△ABC的面积比为:1:3,
则△ABC的面积为:24×3=72(平方厘米),
24+72=96(平方厘米).
答:梯形ABCD的面积是96平方米.
故答案为:96平方厘米.
| 4 |
| 3 |
△ADC的面积:
| 4 |
| 3 |
AD:BC=OA:OC=1:3,因为△ACD与△ABC的底相同,所以△ACD与△ABC的面积比为:1:3,
则△ABC的面积为:24×3=72(平方厘米),
24+72=96(平方厘米).
答:梯形ABCD的面积是96平方米.
故答案为:96平方厘米.
点评:此题利用三角形相似的性质求出图形中线段的比,从而得出对应三角形面积的比,这是计算图形面积时常用的一种手段.

练习册系列答案
相关题目

 已知如图阴影部分的面积是3平方厘米,则两个正方形中较小的正方形的面积为.( )
已知如图阴影部分的面积是3平方厘米,则两个正方形中较小的正方形的面积为.( )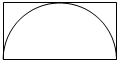 已知如图中长方形的周长是60厘米,求半圆的面积.
已知如图中长方形的周长是60厘米,求半圆的面积. 已知如图线段OC的长度是OA的3倍,三角形DOC的面积是18平方厘米,梯形ABCD的面积是________平方厘米.
已知如图线段OC的长度是OA的3倍,三角形DOC的面积是18平方厘米,梯形ABCD的面积是________平方厘米.