Question

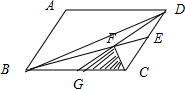如图，平行四边形ABCD的面积是48cm²，CE=2DE，F是DG中点．
①写出图中有哪儿对三角形的面积相等；  
②求出△FGC与△DEF的面积
③求出图中阴影部分的面积．

Answer 1

考点：三角形面积与底的正比关系

专题：平面图形的认识与计算

分析：①由

CB

BG

×

BF

FD

×

DE

EC

=1，得到G是BC中点，又因为F是DG中点，得出6对三角形面积等，又因为ABCD是平行四边形，所以S△_ABD=S△_BDC，因此图中有7对三角形的面积相等．
②根据①面积相等的三角形，得出

△FGC

△DEF

=

△FCE

△DEF

=

CD

DE

=3．再根据平行四边形面积是48，即可求出△FGC与△DEF的面积．
③图中阴影部分的面积是三角形FGC的面积，②已求出．

解答： 解：①由

CB

BG

×

BF

FD

×

DE

EC

=1，得到G是BC中点，又因为F是DG中点，有6对三角形面积等，即：
S△_DCF=S△_GCF，S△_ABD=S△_BCD，S△_BDF=S△_BGF，S△_BDG=S△_CDG，S△_BFG=S△_GFC，
S△_FGC=S△_DFC，
又因为ABCD是平行四边形，所以S△_ABD=S△_BDC，
因此图中有7对三角形的面积相等．

②因为S△_DCF=S△_GCF，S△_ABD=S△_BCD，S△_BDF=S△_BGF，S△_BDG=S△_CDG，S△_BFG=S△_GFC，S△_FGC=S△_DFC，
所以

△FGC

△DEF

=

△FCE

△DEF

=

CD

DE

=3．
因为平行四边形面积是48，
所以S△_FGC=S△_FCD=

1

2

S△_DGC=

1

2

×

1

4

×48=6（平方厘米）．
因为CE=2DE，所以S△_DEF=

1

3

S△_FCD=6×

1

3

=2（平方厘米）．

③图中阴影部分的面积是三角形FGC的面积，即S△_FGC=6（平方厘米）．

点评：此题考查了平行四边形的性质和三角形面积的求解方法．解题的关键是注意当两个三角形等底等高时面积相等．