Question

如图：AD=

1

4

AC，三角形CDE的面积是三角形ABC的一半，问BE的长是BC的几分之几？

Answer 1

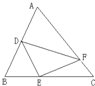
分析：如图：过点E作△CDE的高EF交CD于点F，过点B作△ABC的高交CD于点G，
由AD=

1

4

AC得出DC=

5

4

AC，再根据三角形的面积公式表示出两个三角形的面积，由“三角形CDE的面积是三角形ABC的一半”列出等式，找出两个三角形高的比，从而得CE与BC的比，根据CE+BE=BC，求出BE与BC的比．

解答：解：过点E作△CDE的高EF交CD于点F，过点B作△ABC的高交CD于点G，
因为AD=

1

4

AC，AD+AC=DC，
所以DC=

5

4

AC，
因为S△CDE=

1

2

DC×EF，
所以S△CDE=

1

2

×

5

4

AC×EF=

5

8

AC×EF，
因为S△ABC=

1

2

AC×BG，
又因为S△CDE=

1

2

S△ABC，
所以

5

8

AC×EF=

1

2

×

1

2

AC×BG，
EF=

2

5

BG，
因为EF∥BG，
所以CE=

2

5

BC，
因为CE+BE=BC，
所以

2

5

BC+BE=BC，
          BE=

3

5

BC，
答：BE的长是BC的

3

5

．

点评：此题主要是由条件找出两个三角形高的比，得出CE与BC，再等量代换得出BE与BC的比．