题目内容
 如图,△ABC和△DEC都是等腰直角三角形、四边形EFMN是正方形,则△DEC与△ABC的面积比是
如图,△ABC和△DEC都是等腰直角三角形、四边形EFMN是正方形,则△DEC与△ABC的面积比是8:9
8:9
.分析: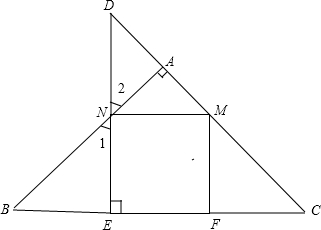
如图:由△ABC和△DEC都是等腰直角三角形、四边形EFMN是正方形,推出FC=MF=MN=DN=NE=BE,∠B=∠D=∠C=∠1=∠2=45°,S△BEN=S△MND,由∠BAC=90°,DN=NM,推出NA是DM的中线,得S△DNA=S△MNA=
S△BEN=
×BE×NE=
EF2,由S△DEC═
×EC×DE=
×2EF×2EF=2EF2,由S△ABC=S△DEC-S△DNA+S△BEN,进行等量代换,找出S△ABC与S△DEC的关系,从而算出它们的面积比.

如图:由△ABC和△DEC都是等腰直角三角形、四边形EFMN是正方形,推出FC=MF=MN=DN=NE=BE,∠B=∠D=∠C=∠1=∠2=45°,S△BEN=S△MND,由∠BAC=90°,DN=NM,推出NA是DM的中线,得S△DNA=S△MNA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:因为△ABC和△DEC都是等腰直角三角形、∠BAC=∠DEC=90°,四边形EFMN是正方形,
所以FC=MF=MN=DN=NE=BE,∠B=∠D=∠C=∠1=∠2=∠FMC=NMD=45°,NA的DM中线,
所以S△DNM=S△BEN=
EF2,
所以S△DNA=S△MNA=
S△BEN=
×
×EF2=
EF2,
因为S△DEC=
EC×DE=
×2EF×2EF=2EF2,
又因为S△ABC=S△DEC-S△DNA+S△BEN,
所以S△ABC=2EF2-
EF2+
EF2,
=
EF2,
所以S△DEC:S△ABC=2EF2:
EF2=8:9,
故答案为:8:9.
所以FC=MF=MN=DN=NE=BE,∠B=∠D=∠C=∠1=∠2=∠FMC=NMD=45°,NA的DM中线,
所以S△DNM=S△BEN=
| 1 |
| 2 |
所以S△DNA=S△MNA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
因为S△DEC=
| 1 |
| 2 |
| 1 |
| 2 |
又因为S△ABC=S△DEC-S△DNA+S△BEN,
所以S△ABC=2EF2-
| 1 |
| 4 |
| 1 |
| 2 |
=
| 9 |
| 4 |
所以S△DEC:S△ABC=2EF2:
| 9 |
| 4 |
故答案为:8:9.
点评:此题关键是利用条件找这两个三角形直角边与正方形边之间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在三角形ABC中,D是BC的一个三等分点,E是AC的中点,AD和BE把三角形分成四块,其面积分别为S1、S2、S3、S4(如图所思)已知S1比S2大7平方厘米,S3的面积为18平方厘米;求△ABC的面积.
在三角形ABC中,D是BC的一个三等分点,E是AC的中点,AD和BE把三角形分成四块,其面积分别为S1、S2、S3、S4(如图所思)已知S1比S2大7平方厘米,S3的面积为18平方厘米;求△ABC的面积. (2006?长汀县)如图,△ABC是等边三角形,D、E分别是AB和AC的中点.△ADE面积是梯形BDEC面积的( )
(2006?长汀县)如图,△ABC是等边三角形,D、E分别是AB和AC的中点.△ADE面积是梯形BDEC面积的( ) 如图,点D、E、F与点G、H、N分别是三角形ABC与三角形DEF各边的中点.那么阴影部分的三角形面积的和是三角形ABC的面积的
如图,点D、E、F与点G、H、N分别是三角形ABC与三角形DEF各边的中点.那么阴影部分的三角形面积的和是三角形ABC的面积的 如图,直线l是对称轴,请你画出和梯形A BCD对称的图形ABC′D′,并用数对表示出梯形ABC′D′四个顶点的位置.
如图,直线l是对称轴,请你画出和梯形A BCD对称的图形ABC′D′,并用数对表示出梯形ABC′D′四个顶点的位置.