题目内容
 把1~8这8个数分别填在右图的8个○内,使每条边上的3个○内数的和相等.其中最小的和是
把1~8这8个数分别填在右图的8个○内,使每条边上的3个○内数的和相等.其中最小的和是12
12
,一共有4
4
种不同的和.分析:根据题意,假设四个顶点商圆圈上填的数分别是A、B、C、D;那么这四条边上的和是:1+2+3+4+5+6+7+8+A+B+C+D=A+B+C+D+36,A、B、C、D是1~8这8个数中的四个,最小是1+2+3+4=10,最大是5+6+7+8=26,然后再进一步解答即可.
解答:解:根据题意,假设四个顶点商圆圈上填的数分别是A、B、C、D,每条边上的3个○内数的和是X;
那么这四条边上的和是:1+2+3+4+5+6+7+8+A+B+C+D=A+B+C+D+36;
又因为A、B、C、D是1~8这8个数中的四个,最小是1+2+3+4=10,最大是5+6+7+8=26,所以,A+B+C+D的和在10~26之间;
又因为每条边上的3个○内数的和相等,那么四条边上的和是4的倍数,36是4的倍数,只要A+B+C+D的和是4的倍数即可;
在10~26之间,是4的倍数的有12,16,20,24;
当A+B+C+D=12时,每条边上的3个○内数的和是:(12+36)÷4=12;1+2+3+6=12,1+3+8=12,3+7+2=12,2+4+6=12,1+5+6=12;可得:
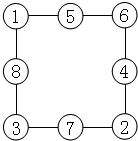 ;
;
当A+B+C+D=16时,每条边上的3个○内数的和是:(16+36)÷4=13;1+4+5+6=16,1+5+7=13,5+6+2=13,6+4+3=13,4+1+8=13;可得:
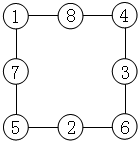 ;
;
当A+B+C+D=20时,每条边上的3个○内数的和是:(20+36)÷4=14;1+8+4+7=20,1+8+5=14,8+4+2=14,4+7+3=14,7+1+6=14;可得:
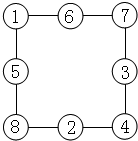 ;
;
当A+B+C+D=24时,每条边上的3个○内数的和是:(24+36)÷4=15;6+8+3+7=24,6+8+1=115,8+3+4=15,3+7+5=15,7+6+2=15;可得:
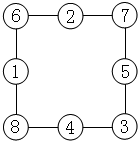 ;
;
由以上可得:一共有4种不同的和,最小的和是12.
故答案为:12,4.
那么这四条边上的和是:1+2+3+4+5+6+7+8+A+B+C+D=A+B+C+D+36;
又因为A、B、C、D是1~8这8个数中的四个,最小是1+2+3+4=10,最大是5+6+7+8=26,所以,A+B+C+D的和在10~26之间;
又因为每条边上的3个○内数的和相等,那么四条边上的和是4的倍数,36是4的倍数,只要A+B+C+D的和是4的倍数即可;
在10~26之间,是4的倍数的有12,16,20,24;
当A+B+C+D=12时,每条边上的3个○内数的和是:(12+36)÷4=12;1+2+3+6=12,1+3+8=12,3+7+2=12,2+4+6=12,1+5+6=12;可得:
 ;
;当A+B+C+D=16时,每条边上的3个○内数的和是:(16+36)÷4=13;1+4+5+6=16,1+5+7=13,5+6+2=13,6+4+3=13,4+1+8=13;可得:
 ;
;当A+B+C+D=20时,每条边上的3个○内数的和是:(20+36)÷4=14;1+8+4+7=20,1+8+5=14,8+4+2=14,4+7+3=14,7+1+6=14;可得:
 ;
;当A+B+C+D=24时,每条边上的3个○内数的和是:(24+36)÷4=15;6+8+3+7=24,6+8+1=115,8+3+4=15,3+7+5=15,7+6+2=15;可得:
 ;
;由以上可得:一共有4种不同的和,最小的和是12.
故答案为:12,4.
点评:本题的关键是求出四个顶点的和是多少,然后再进一步解答即可.

练习册系列答案
相关题目
 你能把1~8这8个数分别填人下图圆圈里,使每一个圆圈上的5个数之和等于20、21或22吗?
你能把1~8这8个数分别填人下图圆圈里,使每一个圆圈上的5个数之和等于20、21或22吗? 把1~8这八个数分别填入图中的八个○内,使每条边上三个○内数的和相等,那么这个和的取值为那些?
把1~8这八个数分别填入图中的八个○内,使每条边上三个○内数的和相等,那么这个和的取值为那些?
