题目内容
 如图,在平行四边形ABCD中,E为DC的中点.DF=2BF.三角形BEF(图中阴影部分)的面积是8平方厘米.求:平行四边形的面积.
如图,在平行四边形ABCD中,E为DC的中点.DF=2BF.三角形BEF(图中阴影部分)的面积是8平方厘米.求:平行四边形的面积.分析:边接CF,△BFE与△CEF的高相同,面积的比就是底的比,E为DC的中点.所以它们面积的比为1:1,△CEF的面积为就是8平方厘米,△BCF与△CDF的高相同,它们面积的比就是底的比,因DF=2BF.所以它们面积积的比是2:1,△CDF的面积是32平方厘米,平行四边形ABCD的面积等于三角形BCD的面积2倍.据此可求出平行四边形的面积.
解答:解:根据分析画图如下:

连接CF,根据分析知:
△BFE与△CEF的高相等,E为DC的中点,BE=CE,它们的底也相同,所以它们的面积相等,
S△BFE=S△CEF=8(平方厘米),
S△BCF=S△BFE+S△CEF=8+8=16(平方厘米),
△BCF与△CDF的高相同,DF=2BF,所以
S△BCF:S△CDF=1:2,
S△CDF=2S△BCF,
S△CDF=2×16,
S△CDF=32(平方厘米),
S△BCD=S△BCF+S△CDF=16+32=48(平方厘米),
S平行四边形ABCD=2×48=96(平方厘米).
答:平行四边形的面积是96平方厘米.

连接CF,根据分析知:
△BFE与△CEF的高相等,E为DC的中点,BE=CE,它们的底也相同,所以它们的面积相等,
S△BFE=S△CEF=8(平方厘米),
S△BCF=S△BFE+S△CEF=8+8=16(平方厘米),
△BCF与△CDF的高相同,DF=2BF,所以
S△BCF:S△CDF=1:2,
S△CDF=2S△BCF,
S△CDF=2×16,
S△CDF=32(平方厘米),
S△BCD=S△BCF+S△CDF=16+32=48(平方厘米),
S平行四边形ABCD=2×48=96(平方厘米).
答:平行四边形的面积是96平方厘米.
点评:本题的关键是根据高相等的三角形面积的比,就它们底的比,来求出三角形的面积.

练习册系列答案
相关题目
 (1)在如图所示方格中画一个直角三角形,其中两个顶点位置分别是A(3,7)和B(1,4),你所画的第三个顶点C位置是( 3,
(1)在如图所示方格中画一个直角三角形,其中两个顶点位置分别是A(3,7)和B(1,4),你所画的第三个顶点C位置是( 3, 如图,在平行四边形中,A、B两点是平行四边形对边上的任意两点,如果甲、乙面积分别是36cm2和30cm2,则丙的面积是
如图,在平行四边形中,A、B两点是平行四边形对边上的任意两点,如果甲、乙面积分别是36cm2和30cm2,则丙的面积是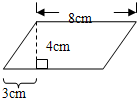 (2010?保靖县)如图,把平行四边形沿高剪开,在把三角形向右平移( )cm,可以得到一个与原图形面积相等的长方形.
(2010?保靖县)如图,把平行四边形沿高剪开,在把三角形向右平移( )cm,可以得到一个与原图形面积相等的长方形.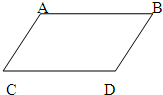 如图是一个平行四边形,(1)过A点画对边CD的垂线,(2)再过D点画对边AB的垂线,(3)在AB上任取一点,画CD的垂线,(4)你发现了什么?
如图是一个平行四边形,(1)过A点画对边CD的垂线,(2)再过D点画对边AB的垂线,(3)在AB上任取一点,画CD的垂线,(4)你发现了什么?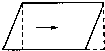 如图,在推导平行四边形面积时,通过平移,把平行四边形转变为长方形.长方形与平行四边形相比( )
如图,在推导平行四边形面积时,通过平移,把平行四边形转变为长方形.长方形与平行四边形相比( )