题目内容
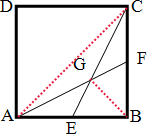
 在正方体ABCD中,E,F分别是所在边的中点,求四边形AGCD的面积占正方形面积的几分之几?
在正方体ABCD中,E,F分别是所在边的中点,求四边形AGCD的面积占正方形面积的几分之几?分析:如图所示,连接AC,BG,则S△ADC=S△ABC=
S正方形,又因E、F分别是所在边的中点,S△AEC=S△ABF=S△CBE=
S△ABC=
S正方形,S△AEG=S△EBG=S△BGF=S△FGC,所以S△AEG=
S△ABF=
×
S正方形=
S正方形,S四边形AGCD=S△ADC+S△AGC=
S正方形+(S△AEC-S△AEG)=
S正方形+(
S正方形-
S正方形)=
S正方形+
S正方形=
S正方形,从而问题得解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |

解答:解:连接AC,BG,则S△ADC=S△ABC=
S正方形,
又因E、F分别是所在边的中点,
所以S△AEC=S△ABF=S△CBE=
S△ABC=
S正方形,
S△AEG=S△EBG=S△BGF=S△FGC,
所以S△AEG=
S△ABF=
×
S正方形=
S正方形,
S四边形AGCD=S△ADC+S△AGC,
=
S正方形+(S△AEC-S△AEG),
=
S正方形+(
S正方形-
S正方形),
=
S正方形+
S正方形,
=
S正方形,
答:四边形AGCD的面积占正方形面积的三分之二.
| 1 |
| 2 |
又因E、F分别是所在边的中点,
所以S△AEC=S△ABF=S△CBE=
| 1 |
| 2 |
| 1 |
| 4 |
S△AEG=S△EBG=S△BGF=S△FGC,
所以S△AEG=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
S四边形AGCD=S△ADC+S△AGC,
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 12 |
=
| 1 |
| 2 |
| 1 |
| 6 |
=
| 2 |
| 3 |
答:四边形AGCD的面积占正方形面积的三分之二.
点评:此题考查组合图形的面积,解决此题的关键是连接BG和AC,转化图形,进行计算.

练习册系列答案
相关题目