题目内容
用一根长128厘米的铁丝,围成一个长宽高的比是4:3:2的长方体框架,这个围成的长方体的表面积是多少?
解:4+3+2=9(份),
长:128÷4× =32×
=32× =
= (厘米),
(厘米),
宽:128÷4×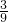 =32×
=32×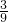 =
= (厘米),
(厘米),
高:128÷4× =32×
=32× =
=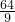 (厘米),
(厘米),
表面积:( +
+ +
+ )×2,
)×2,
(

 )×2,
)×2,
= ×2,
×2,
= ,
,
=657 (平方厘米);
(平方厘米);
答:围成的长方体的表面积是657 平方厘米.
平方厘米.
分析:长方体的棱长总和=(长+宽+高)×4,已知棱长总和是128厘米,长宽高的比是4:3:2,利用按比例分配的方法求此长、宽、高,再根据表面积公式:s=(ab+ah+bh)×2,由此列式解答.
点评:此题主要考查长方体的特征和表面积的计算,关键是已知棱长总和与长、宽、高的比,利用按比例分配的方法求出长、宽、高.
长:128÷4×
 =32×
=32× =
= (厘米),
(厘米),宽:128÷4×
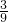 =32×
=32×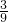 =
= (厘米),
(厘米),高:128÷4×
 =32×
=32× =
=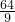 (厘米),
(厘米),表面积:(
 +
+ +
+ )×2,
)×2,(


 )×2,
)×2,=
 ×2,
×2,=
 ,
,=657
 (平方厘米);
(平方厘米);答:围成的长方体的表面积是657
 平方厘米.
平方厘米.分析:长方体的棱长总和=(长+宽+高)×4,已知棱长总和是128厘米,长宽高的比是4:3:2,利用按比例分配的方法求此长、宽、高,再根据表面积公式:s=(ab+ah+bh)×2,由此列式解答.
点评:此题主要考查长方体的特征和表面积的计算,关键是已知棱长总和与长、宽、高的比,利用按比例分配的方法求出长、宽、高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,还剩下多少千克?
,还剩下多少千克?