题目内容
 如图,在以AB为直径的半圆上取一点C,分别以AC和BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置时,图中两个弯月型(阴影部分)AEC和BFC的面积和最大.
如图,在以AB为直径的半圆上取一点C,分别以AC和BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置时,图中两个弯月型(阴影部分)AEC和BFC的面积和最大.分析:观察图形可知,用直径为AC的半圆的面积加上直径为BC的半圆的面积之和减去直径为AB的半圆的面积再加上三角形ABC的面积即可得到两个弯月型阴影部分的面积;结合圆中的一些性质:直径所对的圆周角是直角,以及勾股定理可以得到∠ACB为直角,AC2+BC2=AB2,由此可得两个弯月型阴影部分的面积和就等于三角形ABC的面积,因此问题转化成点C在何处时,三角形ABC的面积最大,依据三角形的面积公式,当底不变时,高越大面积就越大,据此即可解决.
解答:解:由分析知,两个弯月型面积和为:
π×(
)2+
π×(
)2-
π×(
)2+
×AC×BC
=
πAC2+
πBC2-
πAB2+
×AC×BC
=
π(AC2+BC2-AB2)+
×AC×BC
=
×AC×BC;
所以两个弯月型面积和=△ABC的面积.
当△ABC的底不变时,高越大,面积就越大,
所以当点C在圆周的最高处,即在弧AB的中点上时,△ABC的面积最大,此时,两个弯月型面积和也最大.
| 1 |
| 2 |
| AC |
| 2 |
| 1 |
| 2 |
| BC |
| 2 |
| 1 |
| 2 |
| AB |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
=
| 1 |
| 8 |
| 1 |
| 2 |
=
| 1 |
| 2 |
所以两个弯月型面积和=△ABC的面积.
当△ABC的底不变时,高越大,面积就越大,
所以当点C在圆周的最高处,即在弧AB的中点上时,△ABC的面积最大,此时,两个弯月型面积和也最大.
点评:本题难度较大,用到圆的性质以及勾股定理的知识,解决的关键就是能推导出两个弯月型阴影部分的面积和等于三角形ABC的面积.

练习册系列答案
相关题目

 如图,线段AB的长度为10,在AB上任取两点E、F,分别以AE、EF、FB为直径作半圆,设三个半圆的周长的和为m,则m=
如图,线段AB的长度为10,在AB上任取两点E、F,分别以AE、EF、FB为直径作半圆,设三个半圆的周长的和为m,则m= 如图,三角形ABC是直角三角形,AC长4cm,BC长2cm.以AC、BC为直径画半圆,两个半圆的交点D在AB的边上.求阴影部分的面积.
如图,三角形ABC是直角三角形,AC长4cm,BC长2cm.以AC、BC为直径画半圆,两个半圆的交点D在AB的边上.求阴影部分的面积.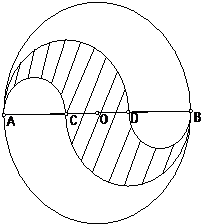 AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积.
AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积.