题目内容
某长方形,长增加
,宽减少
,面积减少
.
| 6 |
| 25 |
| 3 |
| 4 |
| 69 |
| 100 |
| 69 |
| 100 |
分析:设长方形原来的长和宽分别是a和b;根据“长方形的面积=长×宽”计算出原来的长方形的面积;然后根据一个数乘分数的意义,分别计算出后来长方形的长和宽,并根据长方形的面积计算公式计算出后来的面积,进行比较,得出结论.
解答:解:设长方形原来的长和宽分别是a和b,
原来的面积:ab;
增加后的面积:[a×(1+
)]×[b×(1-
)],
=
a×
b,
=
ab;
(ab-
ab)÷ab,
=
ab÷ab,
=
;
答:面积减少
.
故答案为:
.
原来的面积:ab;
增加后的面积:[a×(1+
| 6 |
| 25 |
| 3 |
| 4 |
=
| 31 |
| 25 |
| 1 |
| 4 |
=
| 31 |
| 100 |
(ab-
| 31 |
| 100 |
=
| 69 |
| 100 |
=
| 69 |
| 100 |
答:面积减少
| 69 |
| 100 |
故答案为:
| 69 |
| 100 |
点评:解答此题的关键是先设出原来长方形的长和宽,进而求出变化后的长和宽,根据长方形的面积公式分别求出原来、变化后的面积,进行比较,得出结论.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
一个长方形的长增加了20%,宽减少了20%.那么这个长方形的面积( )
| A、保持不变 | B、减少 | C、减少20% | D、增加20% |
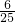 ,宽减少
,宽减少 ,面积减少________.
,面积减少________.