题目内容
平面上6条直线最多将平面分成 部分.
考点:排列组合
专题:综合题
分析:根据一条直线、两条直线、三条直线的情况可总结出规律,从而可得出答案.
解答:
解:由图可知,
(1)有一条直线时,最多分成2部分;
(2)有两条直线时,最多分成2+2=4部分;
(3)有三条直线时,最多分成1+1+2+3=7部分;
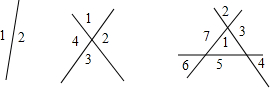
(4)设直线条数有n条,分成的平面最多有m个.有以下规律:
m=1+1+…+(n-1)+n=
+1.
则画6条直线最多可将平面分成
+1=22.
故答案为:22.
(1)有一条直线时,最多分成2部分;
(2)有两条直线时,最多分成2+2=4部分;
(3)有三条直线时,最多分成1+1+2+3=7部分;

(4)设直线条数有n条,分成的平面最多有m个.有以下规律:
m=1+1+…+(n-1)+n=
| n(n+1) |
| 2 |
则画6条直线最多可将平面分成
| 6×7 |
| 2 |
故答案为:22.
点评:本题考查直线与平面的关系,有一定难度,注意培养由特殊到一般再到特殊的探究意识.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
把一个长方体分成几个小长方体后,体积( )
| A、比原来大 | B、比原来小 |
| C、与原来一样大 | D、无法比较 |
