题目内容
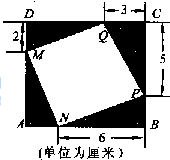如图所示，如果长方形ABCD的面积是56平方厘米，那么四边形MNPQ的面积是多少平方厘米？分析：过M、N、P和Q分别作长方形ABCD的各边的平行线．易知交成中间的红色正方形的边长为3厘米，面积等于9平方厘米．设△MQD、△NAM、△PBN和△QCP的面积之和为S，四边形MNPQ的面积等于x，于是可以得到两个方程X+S=56，X-S=9，联立方程组，即可求解．
解答：
解：如图所示，过M，N，P，Q分别作长方形ABCD的各边的平行线．
易知交成中间的阴影正方形的边长为3厘米，面积等于9平方厘米．
设△MQD，△NAM，△PBN，△QCP的面积之和为S，
四边形MNPQ的面积等于x，
则
解上述方程，得2x=65，所以x=32.5平方厘米．
答：四边形MNPQ的面积是32.5平方厘米．
解：如图所示，过M，N，P，Q分别作长方形ABCD的各边的平行线．易知交成中间的阴影正方形的边长为3厘米，面积等于9平方厘米．
设△MQD，△NAM，△PBN，△QCP的面积之和为S，
四边形MNPQ的面积等于x，
则
|
解上述方程，得2x=65，所以x=32.5平方厘米．
答：四边形MNPQ的面积是32.5平方厘米．
点评：此题属竞赛题，本题考查了不规则四边形的面积求法，解题关键是作出辅助线，求出中间所交正方形的面积，难度较大．
练习册系列答案
孟建平名校考卷系列答案
相关题目
（2012?郑州模拟）甲乙两个同学分别在长方形围墙外的两角（如图所示）．如果他们同时开始绕着围墙逆时针方向跑，甲每秒跑5米，乙每秒跑4米，那么甲最少要跑
如图所示，两个长方形拼成了一个正方形，如果正方形的周长比两个长方形的周长的和少6cm，则正方形的面积是（ ）cm2．
如图所示，用两个长方形纸片和一块正方形纸片拼成大正方形．如果长方形纸片面积分别是44平方厘米与28平方厘米，那么原小正方形的面积是