题目内容

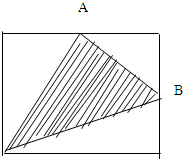
图中A、B两点分别是长方形长和宽的中点，阴影部分面积占长方形面积的

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

B
分析：如图所示，设长方形的长和宽分别为a和b，则三角形FCE的面积为 $\text{[math]}$ ab，三角形ACB的面积为 $\text{[math]}$ $\text{[math]}$ × $\text{[math]}$ a× $\text{[math]}$ b，又因阴影部分的面积=三角形FCE的面积-三角形ACB的面积，据此即可求出阴影部分面积占长方形的面积的几分之几．

解答：阴影部分的面积： $\text{[math]}$ ab- $\text{[math]}$ × $\text{[math]}$ a× $\text{[math]}$ b，
= $\text{[math]}$ ab- $\text{[math]}$ ab，
= $\text{[math]}$ ab；
$\text{[math]}$ ab÷ab= $\text{[math]}$ ；
故选：B．
点评：解答此题的关键是，根据题意，找出三角形FCE与三角形ACB的关系，利用三角形的面积公式，及长方形的特点，即可得出答案．

练习册系列答案

课时练提速训练系列答案

暑假作业光明日报出版社系列答案

黄冈小状元解决问题天天练系列答案

黄冈小状元小秘招系列答案

三点一测快乐周计划系列答案

聚焦课堂四川大学出版社系列答案

暑假作业甘肃教育出版社系列答案

暑假作业大众文艺出版社系列答案

暑假作业吉林教育出版社系列答案

小卷狂练系列答案

相关题目

如图中A，B两点分别是长方形长和宽的中点，阴影部分的面积是36平方厘米，求长方形面积．

图中A、B两点分别是长方形长和宽的中点，阴影部分面积占长方形面积的（　　）

如图是一个周长为50的长方形纸片，A、B两点分别是长和宽的中点．将此长方形沿图中的虚线撕成甲、乙两张．如果甲的周长是48，那么乙的周长是

如图中A，B两点分别是长方形长和宽的中点，阴影部分的面积是36平方厘米，求长方形面积．