题目内容
 如图在梯形ABCD中,两条对角线AC、BD相交于O点,已知AO=
如图在梯形ABCD中,两条对角线AC、BD相交于O点,已知AO=| 1 | 4 |
80
80
cm2.分析:由题意可知:AO=
AC,则三角形AOD的面积就等于三角形ADC的
,于是即可求出三角形ADC的面积,也就能求出三角形DOC的面积,同理,三角形DOC的面积也等于三角形BDC的面积的
,因而可以求出三角形BOC的面积,于是问题即可得解.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:因为AO=
AC,S△AOD=5cm2
所以三角形ADC的面积为5×4=20平方厘米,
三角形DOC的面积就等于20-5=15平方厘米,
三角形BDC的面积等于15×4=60平方厘米,
三角形BOC的面积就等于60-15=45平方厘米,
所以梯形的面积为:5+15+45+15=80平方厘米.
故答案为:80.
| 1 |
| 4 |
所以三角形ADC的面积为5×4=20平方厘米,
三角形DOC的面积就等于20-5=15平方厘米,
三角形BDC的面积等于15×4=60平方厘米,
三角形BOC的面积就等于60-15=45平方厘米,
所以梯形的面积为:5+15+45+15=80平方厘米.
故答案为:80.
点评:解答此题的主要依据是:等高不等底的三角形的面积比就等于其对应底的比.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
 如图在梯形 ABCD中,甲三角形的面积大于乙三角形的面积
如图在梯形 ABCD中,甲三角形的面积大于乙三角形的面积 如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?
如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?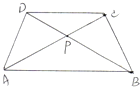 如图在梯形ABCD 中,AB平行于CD,AC与BD 相交于点P,则图中面积相等的三角形共有
如图在梯形ABCD 中,AB平行于CD,AC与BD 相交于点P,则图中面积相等的三角形共有 如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?
如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?