Question

在边长为1的正方形内任取51个点，求证：一定可以从中找出3点，以它们为顶点的三角形的面积不大于1/50．

Answer 1

分析：将边长为1的正方形分成25个边长为

1

5

的正方形，在51个点中，一定有[51÷25]+1=3（个）点属于同一个小正方形； 不妨设A、B、C三点边长为

1

5

三角形在小正方形EFGH内，由于三角形ABC的面积不大于小正方形面积EFGH的

1

2

，又EFGH的面积为

1

5

×

1

5

=

1

25

；故三角形ABC的面积不大于

1

50

；

解答：解：将边长为1的正方形分成25个边长为

1

5

的正方形，在51个点中，一定有[51÷25]+1=3（个）点属于同一个小正方形； 不妨设A、B、C三点边长为

1

5

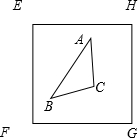
三角形在小正方形EFGH内，由于三角形ABC的面积不大于小正方形面积EFGH的

1

2

，又EFGH的面积为

1

5

×

1

5

=

1

25

；故三角形ABC的面积不大于

1

50

；

点评：此题根据抽屉原理进行解答，抽屉定理是：有N个抽屉，有N+1个物体，必定有且最少有1个抽屉里得放2件物体．